参考吴恩达<机器学习>, 进行 Octave, Python(Numpy), C++(Eigen) 的简单实现.
cost function
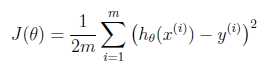
gradient descent
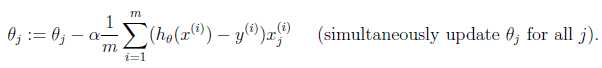
cost function
function J = costFunction(X, Y, theta) m = size(X, 1); predictions = X * theta; sqrErrors = (predictions - Y) .^ 2; J = 1 / (2 * m) * sum(sqrErrors);
Linear regression using gradient descent
function [final_theta, steps, convergence] = gradientDescent(X, Y, init_theta, learning_rate=0.01, max_times=1000, epsilon=0.001) convergence = 0; m = size(X, 1); tmp_theta = init_theta; for i=1:max_times, J_before_update = costFunction(X, Y, tmp_theta); tmp = learning_rate / m * ((X * tmp_theta - Y)‘ * X)‘; tmp_theta -= tmp; J_after_update = costFunction(X, Y, tmp_theta); if abs(J_before_update - J_after_update) <= epsilon, convergence = 1; break; end; end; steps = i; final_theta = tmp_theta;
在这里, 要注意的是, 如何界定是否该停止 Gradient Descent 的迭代, 原则上在训练的末期, 好的迭代应该使 cost function 的值越来越小, 如果震荡, 那就可能是 learning rate 选大了.
可以通过迭代前后 cost function 的值的差来判断是否应该停止迭代, 但是, 如果进行了 feature scaling, 比如 mean normalization, 在 training set 样本很大的情况下, 可能cost function 的值会很小, 差值会更小, 又会造成训练提前停止. 当然这只是简化的描述.
import numpy as np def cost_function(input_X, _y, theta): """ cost function :param input_X: np.matrix input X :param _y: np.array y :param theta: np.matrix theta :return: float """ rows, cols = input_X.shape predictions = np.array(input_X * theta) sqrErrors = (predictions - _y) ** 2 J = 1.0 / (2 * rows) * sqrErrors.sum() return J def gradient_descent(input_X, _y, theta, learning_rate=0.01, max_times=1000, epsilon=0.001): """ gradient descent :param input_X: np.matrix input X :param _y: np.array y :param theta: np.matrix theta :param learning_rate: float learning rate :param max_times: int max iteration times :param epsilon: float epsilon :return: dict """ convergence = 0; rows, cols = input_X.shape for i in range(max_times): J_before = cost_function(input_X, _y, theta) errors = np.array(input_X * theta) - _y delta = 1.0 / rows * (np.matrix(errors).transpose() * input_X).transpose() theta -= learning_rate * delta J_after = cost_function(input_X, _y, theta) if abs(J_before - J_after) <= epsilon: convergence = 1; break steps = i + 1 return {‘theta‘: theta, ‘convergence‘: convergence, ‘steps‘: steps} def generate_data(): """ generate data :return: input_X, y """ input_X, y = np.ones((100, 2)), np.ones((100, 1)) * 7 input_X[:, 0] *= 3 input_X[:, 0] -= np.random.rand(100) / 5 input_X[:, 1] *= 2 input_X[:, 1] -= np.random.rand(100) / 3 y[:, 0] += np.random.rand(100) / 5 return np.matrix(input_X), y def main(): """ main :return: None """ input_X, y = generate_data()
# theta 的初始值必须是 float theta = np.matrix([[0.0], [0.0]]) J = cost_function(input_X, y, theta) print("The return value of cost function is %f" % J) print("The return value of gradient descent is\n") print(gradient_descent(input_X, y, theta)) if __name__ == ‘__main__‘: main()
Python 中需要注意的是, numpy.array, numpy.matrix 和 list 等进行计算时, 有时会进行默认类型转换, 默认类型转换的结果, 往往不是期望的情况.
theta 的初始值必须是 float, 因为如果是 int, 则在更新 theta 时会报错.
#include <iostream> #include <Eigen/Dense> using namespace Eigen; using namespace std; double cost_function(MatrixXd &input_X, MatrixXd &_y, MatrixXd &theta) { double rows = input_X.rows(); MatrixXd predictions = input_X * theta; ArrayXd sqrErrors = (predictions - _y).array().square(); double J = 1.0 / (2 * rows) * sqrErrors.sum(); return J; } class Gradient_descent { public: Gradient_descent(MatrixXd &x, MatrixXd &y, MatrixXd &t, double r=0.01, int m=1000, double e=0.001): input_X(x), _y(y), init_theta(t), theta(t), learning_rate(r), max_times(m), epsilon(e) {} MatrixXd theta; int iterate_times = 1; int convergence = 0; void run(); private: MatrixXd input_X; MatrixXd _y; MatrixXd init_theta; double learning_rate; int max_times; double epsilon; }; void Gradient_descent::run() { double rows = input_X.rows(); for(int i=0; i < max_times; ++i) { double J_before = cost_function(input_X, _y, theta); MatrixXd errors = input_X * theta - _y; MatrixXd delta = 1.0 / rows * (errors.transpose() * input_X).transpose(); theta -= learning_rate * delta; double J_after = cost_function(input_X, _y, theta); iterate_times += 1; if(abs(J_before - J_after) <= epsilon){ convergence = 1; break; } } } int main() { MatrixXd A = MatrixXd::Random(3, 3); MatrixXd y = MatrixXd::Constant(3, 1, 2); MatrixXd theta = MatrixXd::Zero(3, 1); cout << cost_function(A, y, theta) << endl; MatrixXd input_X = MatrixXd::Constant(100, 2, 1); MatrixXd _y = MatrixXd::Constant(100, 1, 7); MatrixXd _theta = MatrixXd::Zero(2, 1); input_X.col(0) *= 3; input_X.col(0) -= VectorXd::Random(100) / 5; input_X.col(1) *= 2; input_X.col(1) -= VectorXd::Random(100) / 3; _y.col(0) += VectorXd::Random(100) / 5; Gradient_descent gd(input_X, _y, _theta); gd.run(); cout << gd.theta << endl << gd.iterate_times << endl << gd.convergence << endl; }
TODO
Linear Regression Using Gradient Descent 代码实现
原文:http://www.cnblogs.com/senjougahara/p/7648398.html