试题:
给定一个带环的链表,找出环起点。
比如:A -> B -> C -> D -> E -> C (C为环形起点)
写一个程序找出环起点C。
ListNode结构如下,请实现 ListNode* find_circle_beginning(ListNode* head);函数,返回环的起点。
struct ListNode { char val; ListNode* next; };
答案:
1、先用快指针(每次走两步)和慢指针(每次走一步),遍历链表,当两个指针相遇时,说明该链表存在环。
2、当两个指针遇到时,慢指针退回到链表起点,快指针保留在相遇点,两个指针都以一次一步前进,再次相遇的点就是环的起点。
源码如下:
ListNode* find_circle_beginning(ListNode* head) { if( head == NULL ) { return NULL; } ListNode* slow = head; ListNode* fast = head; // 寻找相遇点 while( slow != NULL && fast != NULL && fast->next != NULL ) { slow = slow->next; fast = fast->next->next; if( fast == slow ) { // 在此相遇,说明存在环 break; } } // 如果两个指针不等,说明不存在环 if( fast != slow ) { return NULL; } /* 慢指针退回到链表起点,快指针保留在相遇点,两个指针都以一次一步前进,再次相遇的点就是环的起点。 稍后会给出证明 */ slow = head; while( slow != fast ) { slow = slow->next; fast = fast->next; } return fast; }
证明:
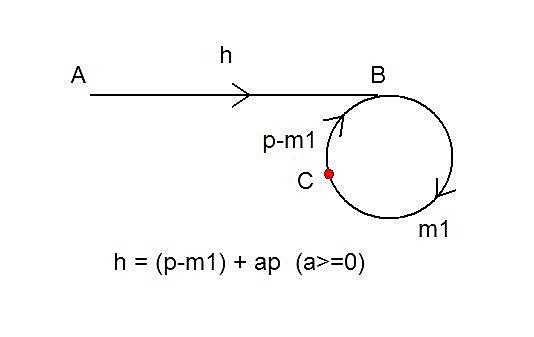
假设环柄长度AB为h,环的长度为p,相遇点为C.
当快指针和慢指针相遇时,慢指针在环上走了m步,总共就是h+m,快指针走过的长度就是2(h+m),在环上走过的长度就是h+2m。在相遇点相遇时,存在以下关系:
(h+2m)%p = m%p
==> ((h+m)+m)%p = m%p
==> (h+m)%p = 0
==> h%p + m%p = p 式(1)
假设BC的长度是m1,则有m%p = m1,带入式(1)得到:
h%p = p - m1
==> h = (p - m1) + ap (a >= 0)
当第二次相遇时,慢指针从头走过h,快指针走(p-m1)+ap,然后在环起点相遇。
小结:
本文的证明实际是倒推的结果。该方法实际上是叫做Pollard‘s Rho Method,详见http://www.csh.rit.edu/~pat/math/quickies/rho/
原文:http://www.cnblogs.com/shokey520/p/3812476.html