主要来自 Scala 语言发明人 Martin Odersky 教授的 Coursera 课程 《Functional Programming Principles in Scala》。
把其他函数作为参数或者作为返回值,就是 higher order functions,python 里面也可以看到这样使用的情形。在酷壳上的博客有一个例子就是将函数作为返回值。
在 python 里边叫 lambda 函数,常常与 map(), filter(), reduce() 联合使用,前面也写过一篇这样的博客。
举一个 scala 的 reduce 的例子,f: Int => Int 表示 f 是一个整数映射到整数的函数,计算下面公式:
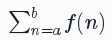
def sum(f: Int => Int, a: Int, b: Int): Int = {
def loop(a: Int, acc: Int): Int =
if (a > b) acc
else loop(a + 1, f(a) + acc)
loop(a, 0)
}
def sumInts(a: Int, b: Int) = sum(x => x, a, b) // f(n)=n
def sumCubes(a: Int, b: Int) = sum(x => x * x * x, a, b) // f(n)=n*n*n
println(sumInts(2, 7)) //求和
println(sumCubes(3, 10)) //求立方和
把一个函数的多个参数分解成多个函数, 然后把函数多层封装起来,每层函数都返回一个函数去接收下一个参数这样,可以简化函数的多个参数。
// sum 返回函数 sumF,风格与 python 相似
def sum(f: Int => Int): (Int, Int) => Int = {
def sumF(a: Int, b:Int): Int =
if (a > b) 0 else f(a) + sumF(a + 1, b)
sumF
}
def sumInts = sum(x => x)
def sumCubes = sum(x => x * x * x)
sumInts(1, 5) //> res0: Int = 15
sumCubes(1, 5) //> res1: Int = 225
sum(x=>x)(1, 5) //> res2: Int = 15
(sum(x=>x))(1, 5) //> res3: Int = 15
更为简短的写法:
def sum(f: Int => Int)(a: Int, b: Int): Int =
if (a > b) 0 else f(a) + sum(f)(a + 1, b)
sum(x => x)(1, 5) // 第一个()相当于创建了一个匿名函数
mapReduce 实现过程包括 map 一一映射函数和 reduce 函数及单位元素 zero(乘为1,加为0),参数包括序列区间 [a, b] 两个参数,假设我们求 [a, b] 区间上所有元素的平方和:
def mapReduce(map: Int => Int, reduce: (Int, Int) => Int, zero: Int)(a: Int, b: Int): Int =
if (a > b) zero
else reduce(map(a), mapReduce(map, reduce, zero)(a + 1, b))
def sumOfSquare(a: Int, b: Int) = mapReduce(x => x*x, (x, y) => x + y, 0)(a, b) //这里确定了三个,留下参数a,b
比如求立方和,四次方和等,更灵活的用法是 map 和 reduce 可以先指定一个reduce(都是sum),使用时再指定另一个(map),代码就不贴了。总之,所有mapreduce设置,包括map,reduce, zero, a, b都可以无序设置,替换组合成包含不同参数列表的新函数。
构造一个分数(rational)类,实现加减、比大小等基本功能。
object rationals {
val x = new Rational(1, 3) //> x : week3.Rational = 1/3
val y = new Rational(5, 7) //> y : week3.Rational = 5/7
val z = new Rational(3) //> z : week3.Rational = 3/1
x.numer //> res0: Int = 1
x.sub(y).sub(z) //> res1: week3.Rational = 71/-21
y.add(y) //> res2: week3.Rational = 10/7
x.less(y) //> res3: Boolean = true
x.max(y) //> res4: week3.Rational = 5/7
}
class Rational(x: Int, y: Int) {
require(y != 0, "denomitor must be nonzero")
// scala 的构造函数就是执行body
def this(x: Int) = this(x, 1) // 第二种构造函数, 补全到第一种
private def gcd(a: Int, b: Int): Int =
if (b==0) a else gcd(b, a % b) //private函数,求最大公约数
val numer = x / gcd(x, y) // 每次构造新类,都化简
val denom = y / gcd(x, y) // val,gcd函数只计算一次
def add(that: Rational) =
new Rational(
numer * that.denom + denom * that.numer, // 交叉相乘相加
denom * that.denom)
def neg: Rational = new Rational(-numer, denom)
def sub(that: Rational) = add(that.neg)
def less(that: Rational) = numer * that.denom < that.numer * denom
def max(that: Rational) = if (this.less(that)) that else this // this 关键字,表示使用该method的object
override def toString = numer + "/" + denom // 每次打印类的格式
}
c++里面有操作符的重载,在scala里面技术层面上来说没有操作符这个概念。比如 1 + 2 实际是 1.+(2)。 + 是对象 1 的一种方法。Scala 实现 1 + 2 这种写法需要两种技术,以上面的例子来分析:
r.add(s) 可以写成 r add s,任何只包含一个参数的方法都可以写成这样的形式,这种做法叫Infix Notation。a + b,分数的加法如果是 a add b,风格不一致。还有一个方法叫 Relaxed Identifiers。大概意思是标志符不仅可以是字母开头的字符串组成,还可以是运算符(如果后面是冒号,加至少一个空格,否则会将冒号也看出标志的一部分)。实现与整数加法风格一致的分数运算,代码如下:
package week3
object rationals {
val x = new Rational(1, 3) //> x : week3.Rational = 1/3
val y = new Rational(5, 7) //> y : week3.Rational = 5/7
val z = new Rational(3) //> z : week3.Rational = 3/1
-x //> res0: week3.Rational = 1/-3
x - y - z //> res1: week3.Rational = 71/-21
y + y //> res2: week3.Rational = 10/7
x < y //> res3: Boolean = true
x * x + z * z //> res4: week3.Rational = 82/9
}
class Rational(x: Int, y: Int) {
require(y != 0, "denomitor must be nonzero")
def this(x: Int) = this(x, 1)
private def gcd(a: Int, b: Int): Int =
if (b==0) a else gcd(b, a % b)
val numer = x / gcd(x, y)
val denom = y / gcd(x, y)
def + (that: Rational) =
new Rational(
numer * that.denom + denom * that.numer,
denom * that.denom)
def unary_- : Rational = new Rational(-numer, denom) // unary_:一元运算符和二元运算符不同,一元要特地指出
def - (that: Rational) = this + -that
def < (that: Rational) = numer * that.denom < that.numer * denom
def * (that: Rational) = new Rational(numer * that.numer, denom * that.denom)
override def toString = numer + "/" + denom // 打印类的格式
}
注意到上面代码中 x*x + z*z 没用括号也能计算出准确的结果,这是因为 scala 通用一套根据标识符确定运算优先级的规则表。
Scala 中的函数式编程基础(二),布布扣,bubuko.com
原文:http://www.cnblogs.com/daniel-D/p/3812795.html