2 10 10 20 20 15 15 25 25.5 0Sample Output
Test case #1 Total explored area: 180.00
题意 :
求一些相交的矩形他们的面积总和 , 重叠的地方只算一次 。
思路 :
推荐博客 : http://www.cnblogs.com/scau20110726/archive/2013/04/12/3016765.html
: http://blog.csdn.net/qq_18661257/article/details/47622677
这题的解法感觉好神奇 , 又学到了一手 。这题要用到扫描线的理念去解题 , 即一根平行于 X 轴或平行于 Y 轴的直线去扫描这个图形,并且给矩形的上下边做上不同的标记,没扫描到一条边时计算一次其最近的的上方的面积。
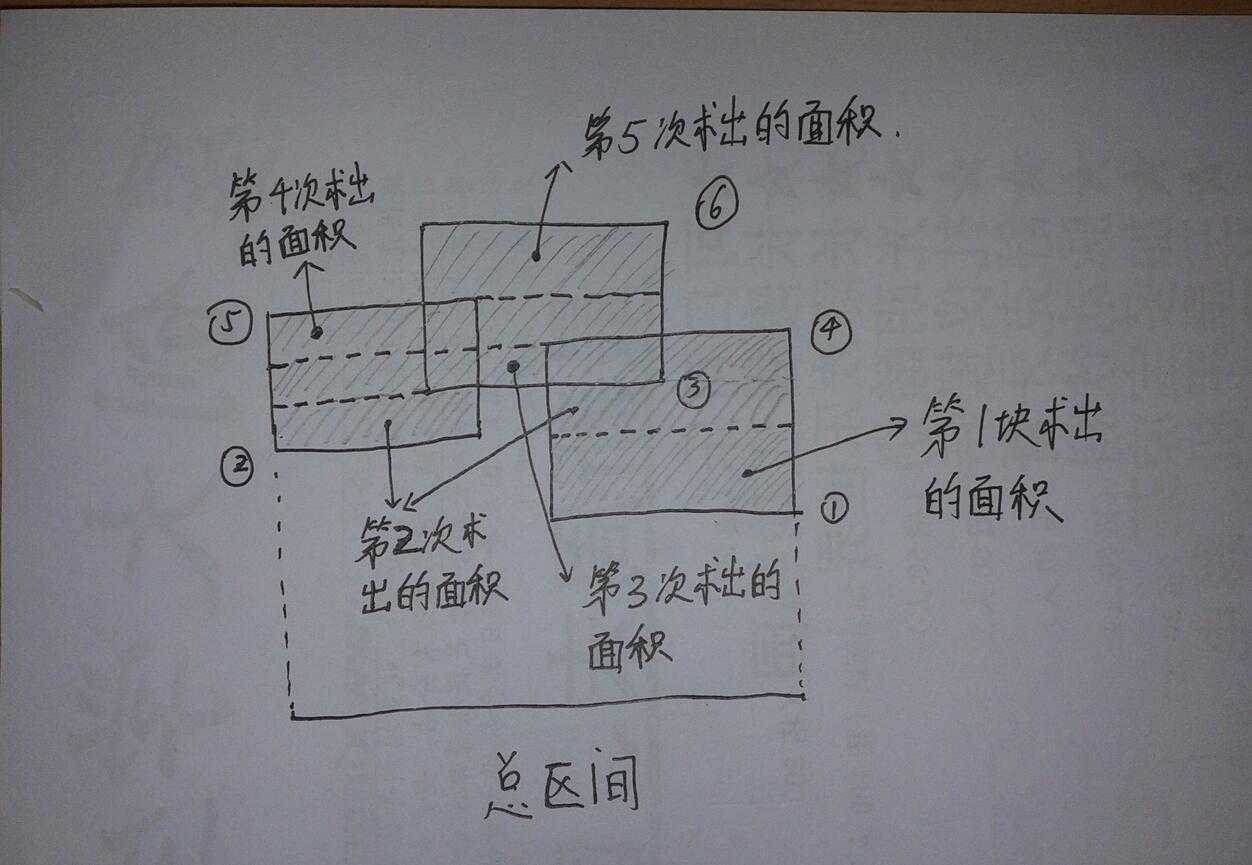
这个题目还有一个问题需要注意, 就是线段树所处理的区间是 [1, a] [a+1, b] [b+1, c] [c+1, d] ,但是这样算相对于此类问题是有缺陷的 , 因为你这样计算后 [a, a+1] 这个区间的长度被你无形中抹去了,造成区间的缺失 , 要怎么去解决呢 ?
在此处可以借助区间的性质 , [ ) , 左闭右开 。 例如你在计算 区间 2 到 4 ,你传过去的区间的参数只需要是 2 到 3 , 然后计算 2 - 2 区间时 , 是 2 - 3 的值, 计算 3 - 3 区间时 , 是 3 - 4 的值。
代码示例 :
/*
* Author: ry
* Created Time: 2017/10/16 18:06:48
* File Name: 3.cpp
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <time.h>
using namespace std;
const int eps = 1e3+5;
const double pi = acos(-1.0);
const int inf = 0x3f3f3f3f;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define ll long long
struct seg
{
double l, r, h;
int pt;
}po[eps];
double pre[eps];
bool cmp(seg a, seg b){
return a.h < b.h;
}
struct node
{
int l, r, f;
double len;
}tree[eps];
void build(int l, int r, int k){
tree[k].l = l;
tree[k].r = r;
tree[k].f = 0, tree[k].len = 0;
if (l == r) return;
int m = (l + r) >> 1;
build(l, m, k<<1);
build(m+1, r, k<<1|1);
}
void down(int k){
if (tree[k].f) {
tree[k].len = pre[tree[k].r+1] - pre[tree[k].l];
}
else if (tree[k].l == tree[k].r) tree[k].len = 0;
else {
tree[k].len = tree[k<<1].len + tree[k<<1|1].len;
}
}
void update(int l, int r, int k, int pt){
if (l <= tree[k].l && tree[k].r <= r){
tree[k].f += pt;
down(k);
return;
}
int m = (tree[k].l + tree[k].r) >> 1;
if (l <= m) update(l, r, k<<1, pt);
if (r > m) update(l, r, k<<1|1, pt);
down(k);
}
int main() {
int n;
double a, b, c, d;
int yy = 1;
while (~scanf("%d", &n) && n){
int k = 1;
for(int i = 1; i <= n; i++){
scanf("%lf%lf%lf%lf", &a, &b, &c, &d);
po[k].l = po[k+1].l = a;
po[k].r = po[k+1].r = c;
po[k].h = b, po[k+1].h = d;
po[k].pt = 1, po[k+1].pt = -1;
pre[k] = a, pre[k+1] = c;
k += 2;
}
sort(pre+1, pre+k);
sort(po+1, po+k, cmp);
int t = 2; // 区间去重,这个地方写一定要注意下
for(int i = 2; i < k; i++){
if (pre[i] != pre[i-1]) pre[t++] = pre[i];
}
build(1, t-1, 1);
double ans = 0;
for(int i = 1; i < k-1; i++){
int l = lower_bound(pre+1, pre+t, po[i].l) - pre;
int r = lower_bound(pre+1, pre+t, po[i].r) - pre - 1;
update(l, r, 1, po[i].pt);
ans += tree[1].len * (po[i+1].h - po[i].h);
}
printf("Test case #%d\n", yy++);
printf("Total explored area: %.2f\n\n", ans);
}
return 0;
}
原文:http://www.cnblogs.com/ccut-ry/p/7679115.html