神tm题目,这几天时间都耗在这道题目上了。
题意:一个森林的权值定义为其树个数的 k 次方,求所有 n 个点的带标号无根
森林的权值和。
对 998244353 取模。
n ≤ 20000 , k ≤ 10



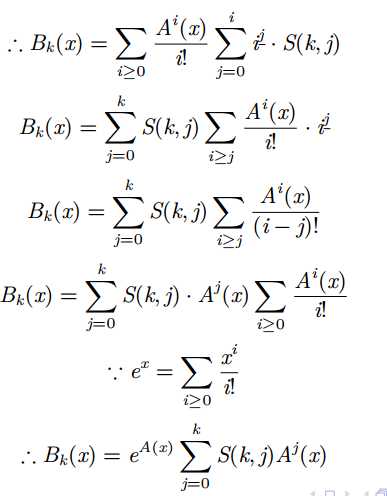

写完之后神清气爽~(注意最后输出的答案是B_k(x)的n次项系数乘上n!)
#include<bits/stdc++.h> #define inf 0x3f3f3f3f #define ll long long #define P 998244353 using namespace std; const int maxn=100010; const int g=3; inline int read(){ int f=1,x=0;char ch=getchar(); while (ch<‘0‘||ch>‘9‘){if (ch==‘-‘)f=-1;ch=getchar();} while (ch>=‘0‘&&ch<=‘9‘){x=(x<<3)+(x<<1)+ch-‘0‘;ch=getchar();} return f*x; } inline int qpow(int x,int p){int ans=1; for(;p;p>>=1,x=1ll*x*x%P)if(p&1)ans=1ll*ans*x%P; return ans; } int n,m,k; int a[maxn],A[maxn],B[maxn],C[maxn],c[maxn],d[maxn],fac[maxn],tmp[maxn],s[11][maxn]; inline void NTT(int *a,int f,int k){ for (int i=0,j=0;i<k;i++){ if (i>j)swap(a[i],a[j]); for (int l=k>>1;(j^=l)<l;l>>=1); } for (int i=1;i<k;i<<=1){ int w=qpow(g,(f*(P-1)/(i<<1)+P-1)%(P-1)); for (int j=0;j<k;j+=(i<<1)){ int e=1; for (int k=0;k<i;++k,e=1ll*e*w%P){ int x,y; x=a[j+k];y=1ll*a[j+k+i]*e%P; a[j+k]=(x+y)%P;a[j+k+i]=(x-y+P)%P; } } } if(f==-1){ int _inv=qpow(k,P-2); for (int i=0;i<k;++i)a[i]=1ll*a[i]*_inv%P; } } inline void GetInv(int *a,int *b,int n){ if (n==1) return void(b[0]=qpow(a[0],P-2)); GetInv(a,b,n>>1); for (int i=0;i<n;++i)tmp[i]=a[i],tmp[n+i]=0; int k;for (k=1;k<=n;k<<=1); for (int i=n;i<k;++i)b[i]=0; NTT(tmp,1,k);NTT(b,1,k); for (int i=0;i<k;++i) tmp[i]=b[i]*(2+P-1ll*tmp[i]*b[i]%P)%P; NTT(tmp,-1,k); for (int i=0;i<n;++i)b[i]=tmp[i],b[n+i]=0; } inline void Getln(int *a,int *b,int *c,int n){ for (int i=0;i<n;++i)b[i]=1ll*(i+1)*a[i+1]%P; GetInv(a,c,n); for (int i=0;i<n;++i)tmp[i]=c[i],tmp[n+i]=0; int k;for (k=1;k<=n;k<<=1); NTT(tmp,1,k);NTT(b,1,k); for (int i=0;i<k;++i) tmp[i]=1ll*b[i]*tmp[i]%P; NTT(tmp,-1,k); for (int i=1;i<=n;++i)b[i]=1ll*tmp[i-1]*qpow(i,P-2)%P,b[i+n]=0;b[0]=0; } inline void Getexp(int *a,int *b,int *c,int *d,int n){ if (n==1)return void(b[0]=1); Getexp(a,b,c,d,n>>1); Getln(b,c,d,n); for (int i=0;i<n;++i)tmp[i]=(a[i]-c[i]+P)%P,tmp[n+i]=0;++tmp[0]; int k;for (k=1;k<=n;k<<=1); NTT(tmp,1,k);NTT(b,1,k); for (int i=0;i<k;++i) tmp[i]=(ll)tmp[i]*b[i]%P; NTT(tmp,-1,k); for (int i=0;i<n;++i)b[i]=tmp[i],b[i+n]=0; } int main(){ a[1]=s[0][0]=fac[0]=1; for (int i=1;i<=10;++i){ for (int j=1;j<=i;++j)s[i][j]=(s[i-1][j-1]+1ll*s[i-1][j]*j%P)%P; } n=read();k=read(); for (int i=2;i<=n;++i)a[i]=qpow(i,i-2); for (int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%P; for (int i=1;i<=n;++i)A[i]=1ll*a[i]*qpow(fac[i],P-2)%P; for (m=1;m<=n;m<<=1); Getexp(A,B,c,d,m); memset(tmp,0,sizeof(tmp)); for (int i=0;i<=n;++i)tmp[i]=A[i]; for (m=1;m<=2*n;m<<=1); NTT(tmp,1,m); for (int i=1;i<=k;++i){ for (int j=0;j<=n;++j)C[j]=(C[j]+1ll*s[k][i]*A[j]%P)%P,A[j+n+1]=0; NTT(A,1,m); for (int j=0;j<=m;++j)A[j]=1ll*A[j]*tmp[j]%P; NTT(A,-1,m); } if (k){ for (int i=n+1;i<=m;++i)B[i]=C[i]=0; NTT(B,1,m);NTT(C,1,m); for (int i=0;i<=m;++i)B[i]=1ll*B[i]*C[i]%P; NTT(B,-1,m); }B[n]=1ll*B[n]*fac[n]%P; printf("%d\n",B[n]); }
原文:http://www.cnblogs.com/szboyi/p/7697701.html