T检测
#计算期望的样本大小
install.packages("pwr")
library(pwr)
pwr.t.test(d=.8,sig.level=.05,power=.9,type="two.sample")
Two-sample t test power calculation
n = 33.82555 #样本大小
d = 0.8 #效应值,标准化的均值之差
sig.level = 0.05 #显著水平
power = 0.9 #功效水平,多少把握成功测量出效果
alternative = two.sided #检测类型,可选的类型为:双侧检测或单侧检测
NOTE: n is number in *each* group
#在固定的样本大小内,结果的正确范围 pwr.t.test(n=20,d=.5,sig.level = .01,type="two.sample")
Two-sample t test power calculation
n = 20
d = 0.5
sig.level = 0.01
power = 0.1439551
alternative = two.sided
NOTE: n is number in *each* group
#方差分析,求期望样本大小 pwr.anova.test(k=5,f=.25,sig.level = .05,power=.8)
Balanced one-way analysis of variance power calculation
k = 5 #分组数量
n = 39.1534 #每组的数据量
f = 0.25 #效应值,
sig.level = 0.05 #显著水平
power = 0.8 #功效
NOTE: n is number in each group
#相关性,求期望样本大小 pwr.r.test(r=.25,sig.level = .05,power=.90,alternative = "greater")
approximate correlation power calculation (arctangh transformation)
n = 133.2803 #样本大小
r = 0.25 #效应值
sig.level = 0.05 #显著水平
power = 0.9 #功效值
alternative = greater
#线性模型,求期望样本大小,N-K-1=样本大小 pwr.f2.test(u=3,f2=0.0769,sig.level =0.05,power=0.90)
Multiple regression power calculation
u = 3 #集合只差
v = 184.2426 #N-变量总数-1=v -> 样本总算=v+变量总数+1
f2 = 0.0769 #效应值
sig.level = 0.05 #显著性
power = 0.9 #功效值
#比例检测,求期望样本大小 pwr.2p.test(h=ES.h(.65,.6),sig.level = .05,power=.9,alternative = "greater")
Difference of proportion power calculation for binomial distribution (arcsine transformation)
h = 0.1033347 #效应值
n = 1604.007 #样本大小
sig.level = 0.05 #显著水平
power = 0.9 #功效值
alternative = greater #测试类型,双尾或单尾
NOTE: same sample sizes
#卡方检验,求期望样本大小 prob<-matrix(c(.42,.28,.03,.07,.10,.10),byrow=TRUE,nrow=3) ES.w2(prob) pwr.chisq.test(w=ES.w2(prob),df=2,sig.level=.05,power=.9)
Chi squared power calculation
w = 0.1853198 #效应值
N = 368.4528 #样本大小
df = 2 #自由度
sig.level = 0.05
power = 0.9
NOTE: N is the number of observations
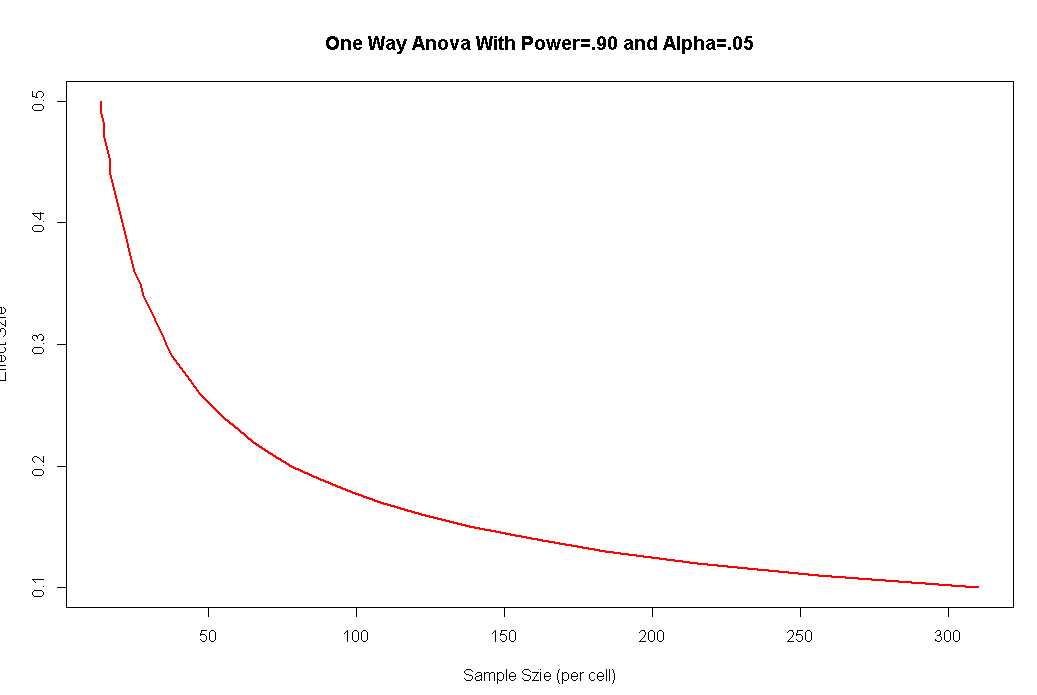
单因素Anova中的检测显著效应所需的样本大小
es<-seq(.1,.5,.01)
nes<-length(es)
samsize<-NULL
for(i in 1:nes){
result<-pwr.anova.test(k=5,f=es[i],sig.level = .05,power=.9)
samsize[i]<-ceiling(result$n)
}
plot(samsize,es,type="l",lwd=2,col="red",ylab="Effect Szie", xlab="Sample Szie (per cell)",main="One Way Anova With Power=.90 and Alpha=.05")
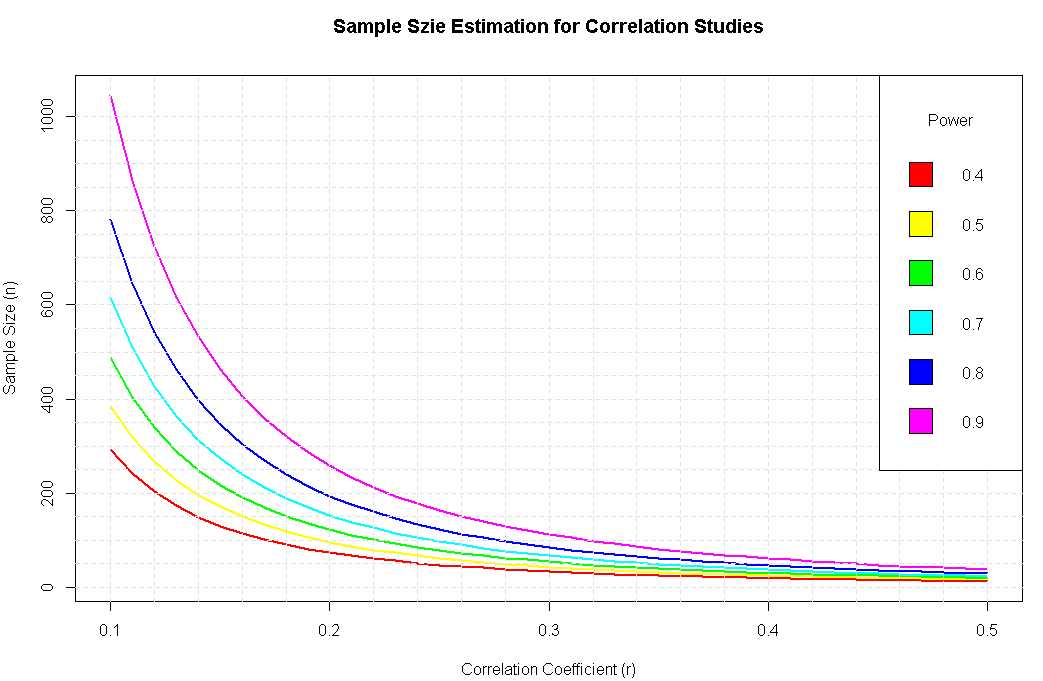
r<-seq(.1,.5,.01)#在.1和.5之间生成步长为.01的数字序列
nr<-length(r)
p<-seq(.4,.9,.1)
np<-length(p)
samsize<-array(numeric(nr*np),dim=c(nr,np))
#samsize
for(i in 1:np)
{
for(j in 1:nr)
{
result<-pwr.r.test(n=NULL,r=r[j],sig.level = .05,power = p[i],alternative = "two.sided")
samsize[j,i]<-ceiling(result$n)
}
}
# samsize
xrange<-range(r)
yrange<-round(range(samsize))
colors<-rainbow(length(p))
plot(xrange,yrange,type="n",xlab="Correlation Coefficient (r)",ylab="Sample Size (n)")
for(i in 1:np){
lines(r,samsize[,i],type="l",lwd=2,col=colors[i])
}
abline(v=0,h=seq(0,yrange[2],50),lty=2,col="grey89")
abline(h=0,v=seq(xrange[1],xrange[2],.02),lty=2,col="gray89")
title("Sample Szie Estimation for Correlation Studies\n")
legend("topright",title="Power",as.character(p),fill=colors)
何为显著性检验
显著性检验的思想十分的简单,就是认为小概率事件不可能发生。虽然概率论中我们一直强调小概率事件必然发生,但显著性检验还是相信了小概率事件在我做的这一次检验中没有发生。
显著性检验即用于实验处理组与对照组或两种不同处理的效应之间是否有差异,以及这种差异是否显著的方法。
常把一个要检验的假设记作H0,称为原假设(或零假设),与H0对立的假设记作H1,称为备择假设。
⑴在原假设为真时,决定放弃原假设,称为第一类错误,其出现的概率通常记作α;
⑵在原假设不真时,决定接受原假设,称为第二类错误,其出现的概率通常记作β。
通常只限定犯第一类错误的最大概率α,不考虑犯第二类错误的概率β。这样的假设检验又称为显著性检验,概率α称为显著性水平。
原文:http://www.cnblogs.com/GhostBear/p/7736102.html