【问题描述】
你是一名优秀的水管工。 一天你遇到了一个棘手的难题。 你需要在一个长方体状的房间
内连接一条贯穿房间内部的水管。房间的长为 X,宽为 Y,高为 Z, 整个房间可以看成是 X×Y×Z
个小立方体空间组成的。 如果位房间建立直角坐标系,则房间内每个小立方体空间都可以用
一个三维坐标(x,y,z)表示, 房间一角的小立方体的坐标为(1,1,1), 它的对角的坐标为(X,Y,Z),
其余小立方体的坐标的三个维度都分别落在 1…X, 1…Y 和 1…Z 内。 水管的入口和出口已经
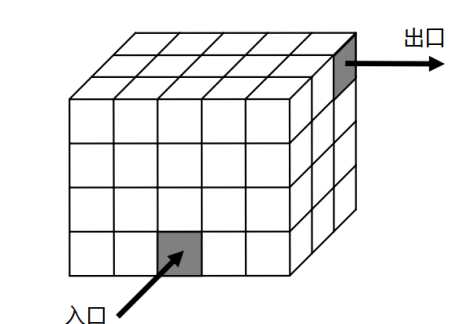
开凿好了,它们位于长方体的表面(可能位于房间的地板、墙壁或天花板上),且正好占据
了某个小立方体的一个面。下图展示了房间的立方体空间的划分方式和一种开凿水管出入口
的方式。
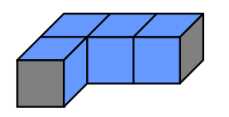
你的手头只有一种形状的水管部件, 它呈 L 型,且正好占据了 4 个小立方体空间, 如下
图所示, 灰色部分是水管部件两端的开口位置。
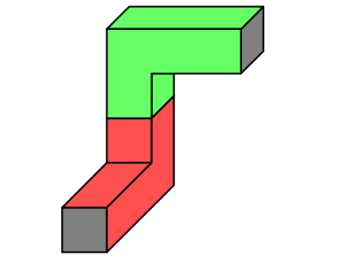
你可以任意旋转、翻转水管部件,然后将它的开口接到入口、 出口或者其它水管部件的
开口上。 水管的开口必须正好接在入口或出口上才算接上,伸出房间外一截是不行的。 下图
展示了一种两个水管部件的连接方式。
在连接水管时, 水管部件间不能相交,也不能伸出房间之外。房间内有一些小立方体空
间已经被物品占据了,水管也不能经过那些格子。 另外,水管部件数量有限,你的手头只有
12 个这样的零件。
现在,给出房间的长、高、 宽, 以及入口、出口的位置和房间内物品的坐标,请你计算 至少需要多少个这样的水管部件才能完成任务,或者判断无法完成任务。
【输入】
输入的第 1 行包含 4 个正整数 X, Y, Z, m,其中 X,Y,Z 表示房间的长、高、宽, m 表示
房间中物品的数量。
输入的第 2 行包含 3 个正整数 x1, y1, z1, 和一个字符 ch。 其中(x1,y1,z1)是水管入口所
在的小立方体的坐标。 ch 的值为‘x‘、 ‘y‘或‘z‘, 用于指示入口所在的面。 当 ch 为‘x‘时,表示
入口所在的面与 YZ 坐标平面平行, 当 ch 为‘y‘时,表示入口所在的面与 XZ 坐标平面平行,
当 ch 为‘z‘时,表示入口所在的面与 XY 坐标平面平行。 输入保证入口所在的面在长方体表面
上。 数字和数字、数字和字符间用一个空格隔开。
输入的第 3 行包含 3 个正整数 x2, y2, z2,和一个字符 ch, 表示水管出口的位置, 意义
与格式同上。
接下来 m 行,每行包含三个正整数 xi, yi, zi,表示在坐标(xi,yi,zi)的小立方体空间内有
物品。
【输出】
输出包含 1 个整数,表示最少使用的水管部件的数量。 如果不能完成接水管的任务,输
出“impossible”, 不含引号。
【输入输出样例 1】
| plumber.in | plumber.out |
| 5 4 3 1 3 1 1 z 1 4 3 x 2 3 3 |
2 |
见选手目录下的 plumber/plumber1.in 与 plumber/plumber1.out
【输入输出样例 1 说明】
入口和出口的位置如图所示: 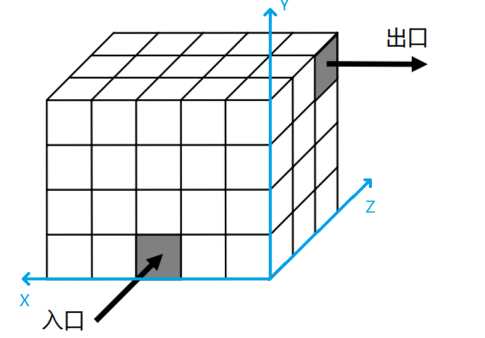

分析:就是一道爆搜题.dfs,记录放的水管的最后一个位置和方向,除了这个方向和它对面的方向以外都可以放,然后就有两种方式了,讨论一下,枚举一下旋转方向就行了.
直接搜会T掉,要加上剪枝.可行性剪枝似乎不行,考虑最优性剪枝,如果剪枝仅仅是如果当前用的水管数>ans就返回,还是会T掉4个点,需要用上一个估价函数.考虑3维空间上的曼哈顿距离,每用一个水管当前位置与终点位置的曼哈顿距离就会-4,计算一下当前点与终点的曼哈顿距离为多少就能计算出至少还需要用多少根水管,就能最优性剪枝了.
#include <map> #include <cmath> #include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int dx[] = { 1, -1, 0, 0, 0, 0 }, dy[] = { 0, 0, 1, -1, 0, 0 }, dz[] = { 0, 0, 0, 0, 1, -1 }; int X, Y, Z, m, ans = 13, tx, ty, tz, tdir, sx, sy, sz, sdir; bool vis[30][30][30], a[30][30][30]; bool check(int x, int y, int z) { if (x >= 1 && x <= X && y >= 1 && y <= Y && z >= 1 && z <= Z && !vis[x][y][z] && !a[x][y][z]) return true; return false; } void dfs(int x, int y, int z, int dir, int p) { int dis = abs(tx - x) + abs(ty - y) + abs(tz - z); if (p + dis / 4>= ans) return; if (x == tx && y == ty && z == tz && dir == tdir) { ans = min(ans, p); return; } if (check(x + dx[dir], y + dy[dir], z + dz[dir]) && check(x + 2 * dx[dir], y + 2 * dy[dir], z + 2 * dz[dir])) { vis[x + dx[dir]][y + dy[dir]][z + dz[dir]] = 1; vis[x + 2 * dx[dir]][y + 2 * dy[dir]][z + 2 * dz[dir]] = 1; int nx = x + 2 * dx[dir], ny = y + 2 * dy[dir], nz = z + 2 * dz[dir]; for (int i = 0; i < 6; i++) { if ((i / 2) != (dir / 2)) { if (check(nx + dx[i], ny + dy[i], nz + dz[i]) && check(nx + 2 * dx[i], ny + 2 * dy[i], nz + 2 * dz[i])) { vis[nx + dx[i]][ny + dy[i]][nz + dz[i]] = vis[nx + 2 * dx[i]][ny + 2 * dy[i]][nz + 2 * dz[i]] = 1; dfs(nx + 2 * dx[i], ny + 2 * dy[i], nz + 2 * dz[i], i, p + 1); vis[nx + dx[i]][ny + dy[i]][nz + dz[i]] = vis[nx + 2 * dx[i]][ny + 2 * dy[i]][nz + 2 * dz[i]] = 0; } } } if (check(x + 3 * dx[dir], y + 3 * dy[dir], z + 3 * dz[dir])) { vis[x + 3 * dx[dir]][y + 3 * dy[dir]][z + 3 * dz[dir]] = 1; int nx = x + 3 * dx[dir], ny = y + 3 * dy[dir], nz = z + 3 * dz[dir]; for (int i = 0; i < 6; i++) { if ((i / 2) != (dir / 2)) { if (check(nx + dx[i], ny + dy[i], nz + dz[i])) { vis[nx + dx[i]][ny + dy[i]][nz + dz[i]] = 1; dfs(nx + dx[i], ny + dy[i], nz + dz[i], i, p + 1); vis[nx + dx[i]][ny + dy[i]][nz + dz[i]] = 0; } } } vis[x + 3 * dx[dir]][y + 3 * dy[dir]][z + 3 * dz[dir]] = 0; } vis[x + dx[dir]][y + dy[dir]][z + dz[dir]] = 0; vis[x + 2 * dx[dir]][y + 2 * dy[dir]][z + 2 * dz[dir]] = 0; } } int main() { scanf("%d%d%d%d", &X, &Y, &Z, &m); char s[2]; scanf("%d%d%d", &sx, &sy, &sz); scanf("%s", s); sdir = (s[0] - ‘x‘) * 2; //找起点 if (s[0] == ‘x‘) sdir += (sx == X); else if (s[0] == ‘y‘) sdir += (sy == Y); else if (s[0] == ‘z‘) sdir += (sz == Z); sx -= dx[sdir]; sy -= dy[sdir]; sz -= dz[sdir]; scanf("%d%d%d", &tx, &ty, &tz); scanf("%s", s); tdir = (s[0] - ‘x‘) * 2; if (s[0] == ‘x‘) tdir += (tx == 1); else if (s[0] == ‘y‘) tdir += (ty == 1); else if (s[0] == ‘z‘) tdir += (tz == 1); for (int i = 1; i <= m; i++) { int x, y, z; scanf("%d%d%d", &x, &y, &z); a[x][y][z] = 1; } dfs(sx, sy, sz, sdir, 0); if (ans == 13) printf("impossible\n"); else printf("%d\n", ans); return 0; }
原文:http://www.cnblogs.com/zbtrs/p/7739504.html