一、四元数
四元数本质上是个高阶复数,可视为复数的扩展,表达式为y=a+bi+cj+dk。在说矩阵旋转的时候提到了它,当然四元数在Unity里面主要作用也在于此。在Unity编辑器中的Transform组件,包括这位置(Position)、旋转(Rotation)和缩放(Scale).Rotation就是一个四元数,但是不能直接对Quaterian.Rotation赋值。可以使用函数Quaterian.Eular(Vector3 angle)获取四元数,该函数返回的就是四元数。
欧拉角表示为Quaterion.eulerAngles,欧拉角可以对其进行赋值,例如
Quaterion.eulerAngles=new Vector3(0,30,0);
四元数可以用来进行旋转,它的表达式为Quaterion.AngleAxis(float angle,Vector3 axis),调用这个函数可以对物体进行旋转,当然还需要调用函数Quaternion.Lerp()在旋转时进行插值计算,这些函数都是在编写逻辑时调用的。
如果对于四元数理解的不够清楚,推荐阅读这篇文章Understanding Quaternion中文翻译 http://www.qiujiawei.com/understanding-quaternions/
二、欧拉角
欧拉角也是用于旋转的,但是它有一个致命的缺点,就是万向节死锁,欧拉角旋转我们在Unity开发中通常使用的函数是transform.Rotate(Vector3 angle)
万向节死锁就是在3D空间中某两个轴在旋转时重叠了,不论你如何旋转,三个轴就变成了两个轴。举个例子:
transform.Rotate(new Vector3(0,0,40));
transform.Rotate(new Vector3(0,90,0));
transform.Rotate(new Vector3(80,0,0));
我们只需要固定中间一句代码,即使y轴的旋转角度始终为90°,那么你会发现无论怎么样调整x轴和z轴的旋转角度,它们会总是在同一个平面上运动。万向节锁实际上并没有锁住任何一个旋转轴,知识在这种情况下会感觉丧失了一个维度。以上面的例子还说,尽管固定了第二个旋转轴的角度为90°,但我们原以为依靠改变其他两个州的旋转角度是可以得到任意旋转位置的(因为按照我们的理解,两个周应该控制两个空间维度),而事实是它被锁在一个平面上了,即只有一个维度了,缺失了一个维度。而只要第二个旋转轴不是正负90°,我们就可以依靠改变其他两个轴的旋转角度来的到任意旋转位置。
从最简单的理解,还是用x,y,z的旋转顺序。当y轴的旋转角度为90°时,会得到下面的矩阵。
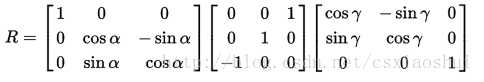
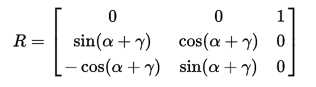
在改变第一次和第三次的旋转角度时,同样的效果,不会改变第一行和第三列的数值,从而缺失了一个维度。究其出现的本质原因,是因为从欧拉角到旋转的映射并不是一个覆盖映射,即不同的欧拉角可以表示同一个旋转方向,而且并不是每一个旋转变化都可以用欧拉角来表示的。
原文:http://www.cnblogs.com/sherryke/p/7739732.html