二次方程优化（二）之 Quadratic Form

我们这一次对二次型进行更深的讨论

讨论多变量的正定型、负定型和半正定、半负定

先给出结论：

判断有两种方法：

1.强推特征值法：如果所有的特征值是正，则是正定型；全是负的就是负定型；全是非负，就是半正定型；全是非正，就是半负定型；

2.子式判断法：分两步：

　　第一步：所有阶的主子式大于0，就是正定型；奇数阶的主子式小于0并且偶数阶的主子式大于0，就是负定型；所有阶的主子式大于等于0或者奇数阶的主子式小于等于0并且偶数阶的主子式大于等于0，转入第二步；除此之外的都是不定型；

　　第二步：所有阶的子式大于等于0，就是半正定型；奇数阶的子式小于等于0并且偶数阶的子式大于等于0，就是半负定型

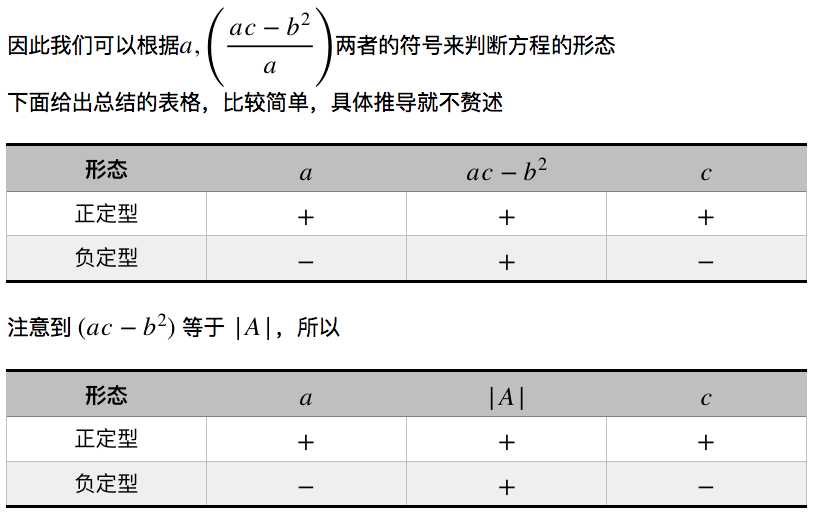
在继续下面的讨论时，我想先插入一小段关于相关矩阵的一些说明

二次方程优化（二）之 Quadratic Form

原文：http://www.cnblogs.com/Mr-ZeroW/p/7748581.html