弧度
弧度π=角度180°
坐标表示法(a,b)的含义
大概就是:从(0,0)向(a,b)连一条有向线段,它表示的向量就与向量(a,b)相等。
或者:$(a,b)=ai+bj$,就是正交分解成两个分别与x、y轴同向的单位向量
点b与点a相减
直接两组坐标对应减即可,得到向量,得到一个方向为a到b的方向,长度为a与b的直线距离的向量
向量与数的乘/除
直接两个坐标乘/除该数字即可,得到向量,几何意义:方向不变,长度乘/除(本文中*号表示数乘)
点与向量的加/减
直接两组坐标对应加/减即可,得到点,几何意义:以该点为起点,沿着向量方向移动向量长度
向量与向量的加/减
直接两组坐标对应加/减即可,得到向量,几何意义:满足平行四边形法则/三角形法则
向量相同
长度相等且方向相同
向量共线(或称“平行”)
就是方向相同或相反,长度不管。判定:叉积为0
向量a与向量b的内积/点积/数量积(?)(返回一个数量)
a的长度*b的长度*cos夹角,$a{\cdot}b=|a||b|cos\theta$
这里的夹角指从a到b逆时针旋转的角,因此夹角绝对值大于90°时点积为负。
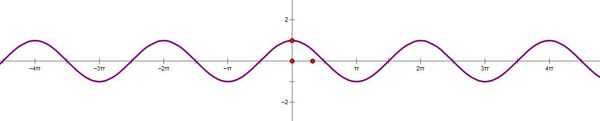
($cos{\theta}$图像)
几何意义:a的长度*b在a的方向上的投影
满足:
交换律,分配律,结合律(可以几何证明)
垂直向量的内积为0。
a与b同向,那么内积等于长度的乘积。
a与b反向,那么内积等于长度乘积的相反数。
坐标计算:
设$a=x1*i+y1*j,b=x2*i+y2*j$,
那么$a{\cdot}b=(x1*i+y1*j){\cdot}(x2*i+y2*j)$
$=x1*x2*i^2+x1*y2*i*j+y1*x2*i*j+y1*y2*j^2$
由于i,j垂直且长度为1,那么$i^2=j^2=1$,$i{\cdot}j=j{\cdot}i=0$
所以$a{\cdot}b=x1*x2+y1*y2$
向量夹角
用内积计算式变换一下即可。
${\theta}=a{\cdot}b/(|a||b|)$
向量长度(也叫“模”)
就是自身内积开平方根。
$|a|=\sqrt{a{\cdot}a}$
也可以理解为勾股定理。
向量a与向量b的叉积/外积(×)(返回一个向量)
(似乎一般只使用这个向量的长度也就是一个数量...)
$a{\times}b=|a||b|sin{\theta}$,就是三角形面积的某个公式乘2
$a{\times}b=a.x*b.y-b.x*a.y$
满足:
反交换律$a{\times}b=-b{\times}a$
分配律$a{\times}(b+c)=a{\times}b+a{\times}c$
结合律$(r*a){\times}b=a{\times}(r*b)=r(a{\times}b)$
几何意义:
把a和b的起点固定,a和b组成的三角形的“有向面积”的两倍,就是形成的一个平行四边形的面积。
所谓有向面积,如果从a到b旋转是逆时针,那么为正,如果是顺时针则为负(旋转取小于等于180°的角)。
或者说,沿着a的方向看,b在左侧,那么为正,如果在右侧则为负。
如果a、b共线,不管方向相同还是相反,叉积都为0。
向量旋转
设rad为逆时针旋转的角度(弧度制),那么新向量为$(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad))$
在2-D的迪卡尔坐标系中,一个位置向量的旋转公式可以由三角函数的几何意义推出。比如上图所示是位置向量R逆时针旋转角度B前后的情况。在左图中,我们有关系:
x0 = |R| * cosA
y0 = |R| * sinA
=>
cosA = x0 / |R|
sinA = y0 / |R|
在右图中,我们有关系:
x1 = |R| * cos(A+B)
y1 = |R| * sin(A+B)
其中(x1, y1)就是(x0, y0)旋转角B后得到的点,也就是位置向量R最后指向的点。我们展开cos(A+B)和sin(A+B),得到
x1 = |R| * (cosAcosB - sinAsinB)
y1 = |R| * (sinAcosB + cosAsinB)
现在把
cosA = x0 / |R|
sinA = y0 / |R|
代入上面的式子,得到
x1 = |R| * (x0 * cosB / |R| - y0 * sinB / |R|)
y1 = |R| * (y0 * cosB / |R| + x0 * sinB / |R|)
=>
x1 = x0 * cosB - y0 * sinB
y1 = x0 * sinB + y0 * cosB
这样我们就得到了2-D迪卡尔坐标下向量围绕原点的逆时针旋转公式。
直线的参数表示
$P+tv$,其中P为点,t为参数,v为向量(表示方向)
直线:t无限制;射线:t大于0;线段:t在0和1之间
直线交点
设直线分别为$P+tv$和$Q+tw$。交点在第一条直线上参数为t1,第二条直线上参数为t2。
那么,$P+t1v=Q+t2w$
两边同时叉乘w,得到$(P+t1v){\times}w=(Q+t2w){\times}w$
由分配律知,$P{\times}w+t1v{\times}w=Q{\times}w+t2w{\times}w$
由结合律(?)知,$P{\times}w+t1v{\times}w=Q{\times}w+t2(w{\times}w)$
由$w×w=0$知,$P{\times}w+t1v{\times}w=Q{\times}w$
则$t1v{\times}w=Q{\times}w-P{\times}w=(Q-P){\times}w=w{\times}(P-Q)$
则$t1=(w{\times}(P-Q))/(v{\times}w)=cross(w,P-Q)/cross(v,w)$
点到直线距离
简单,画图验证即可。基本就是直线上任取一点,叉积算出某个平行四边形的面积,再除以底。
直线上有点A、B,P到直线的距离是$(B-A){\times}(P-a)/|(B-A)|$
如果不取绝对值,那么返回的是有向距离:
//(未验证)沿直线上两点形成有向线段方向看去,如果点在右侧那么为负,如果点在左侧则为正。
namespace X { const double eps=1e-10; struct Point { double x,y; Point(double x=0,double y=0):x(x),y(y){} }; typedef Point Vec; Vec operator+(const Vec& a,const Vec& b) { return Vec(a.x+b.x,a.y+b.y); } Vec operator-(const Vec& a,const Vec& b) { return Vec(a.x-b.x,a.y-b.y); } Vec operator*(const double& a,const Vec& b) { return Vec(a*b.x,a*b.y); } Vec operator*(const Vec& a,const double& b) { return Vec(b*a.x,b*a.y); } Vec operator/(const Vec& a,const double& b) { return Vec(a.x/b,a.y/b); } int dcmp(double x) { if(fabs(x)<eps) return 0; return x<0?-1:1; } bool operator==(const Vec& a,const Vec& b) { return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0; } double dot(const Vec& a,const Vec& b) { return a.x*b.x+a.y*b.y; } double len(const Vec& x) { return sqrt(dot(x,x)); } double angle(const Vec& a,const Vec& b) { return acos(dot(a,b)/len(a)/len(b)); } double cross(const Vec& a,const Vec& b) { return a.x*b.y-a.y*b.x; } Vec Rotate(const Vec& a,const double& rad) { return Vec(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad)); } Point get_line_intersection(const Point& p,const Vec& v,const Point& q,const Vec& w) { return p+v*cross(w,p-q)/cross(v,w); } double dis_to_line(const Point& p,const Point& a,const Point& b) { Vec v1=b-a,v2=p-a; return fabs(cross(v1,v2)/len(v1)); } double dis_to_seg(const Point& p,const Point& a,const Point& b) { if(a==b) return len(p-a); Vec v1=b-a,v2=p-a,v3=p-b; if(dcmp(dot(v1,v2))<0) return len(v2); else if(dcmp(dot(v1,v3))>0) return len(v3); else return fabs(cross(v1,v2)/len(v1)); } };
原文:http://www.cnblogs.com/hehe54321/p/7761866.html