当n个编号元素以某种顺序进栈,并可在任意时刻出栈,所获得的编号元素排列的数目N恰好满足Catalan函数的计算,即N=C(2n,n)/(n+1)。
卡特兰数又称卡塔兰数,是组合数学中一个常出现在各种计数问题中的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名。
卡特兰数的前几项:1,1,2,5,14,42,132,429,1430,4862…
卡特兰数原理:
令h(0)=1,h(1)=1,catalan数满足递推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
该递推关系的解为:h(n) = C(2n,n)/(n+1),n=0,1,2,3,... (其中C(2n,n)表示2n个物品中取n个的组合数)
例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为:
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为:
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
思考:观察Catalan的结构,每个分量都由两个部分相乘(具有递归性质)
卡特兰数应用之出栈次序:
问题一:
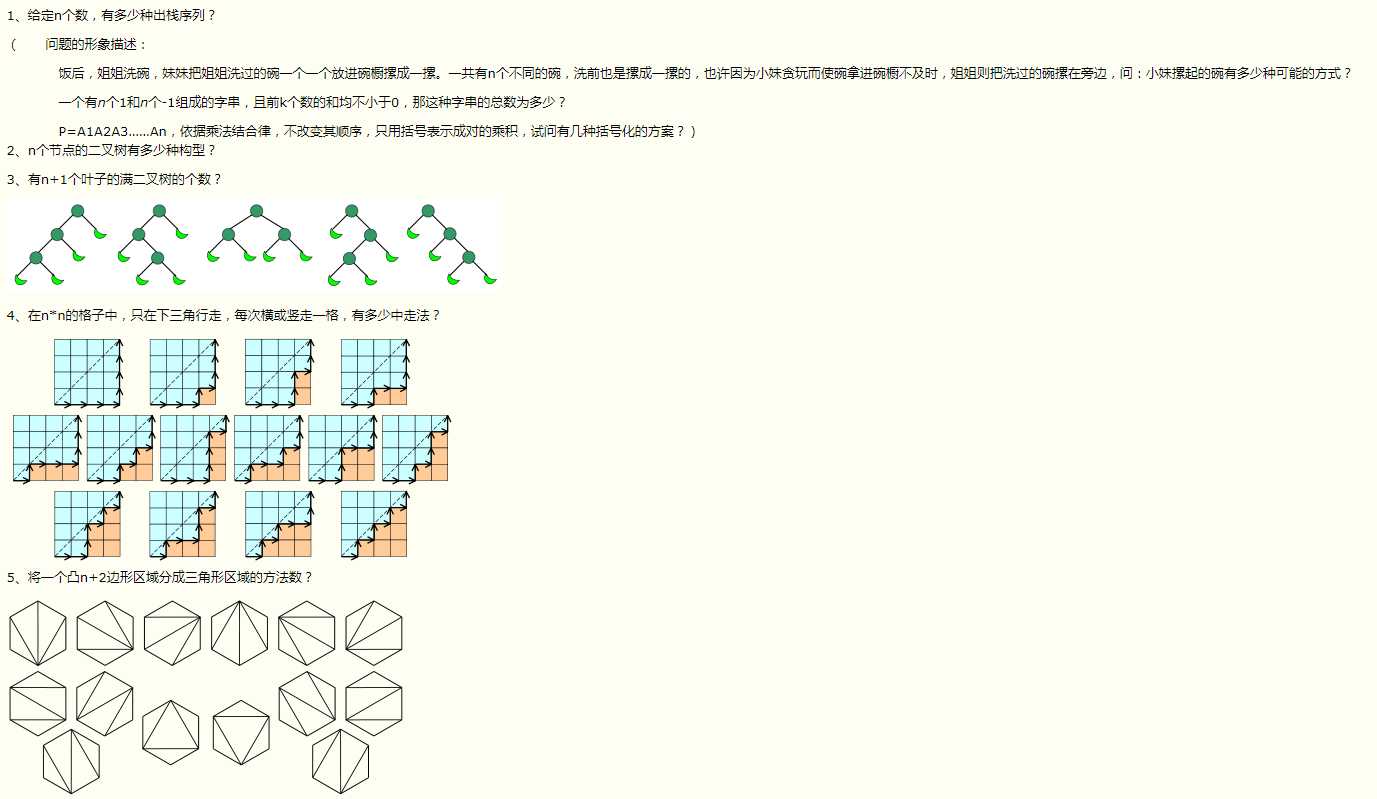
一个栈的进栈序列为1,2,3,…,n。有多少个不同的出栈序列?
分析:设f(n) = 序列个数为n的出栈序列种数。设最后出栈的元素为k。即在k进栈之前,元素1,2,…,k-1已经出栈,出栈序列数为f(k-1)。在k进栈后,元素k+1,k+2,…,n已经进栈后全部出栈。所以元素k+1,k+2,…,n出栈序列种数为f(n-k)。由于比k小和比k大的值入栈出栈情况是相互独立的,此处可用乘法原则,f(n-k)*f(k-1)种,求和便是Catalan递归式。
解决:f(n) = f(n-k)*f(k-1),其中k=1,2,3,…,n 所以f(n) = h(n)= C(2n,n)/(n+1) = c(2n,n)-c(2n,n+1)(n=0,1,2,3,…,n)
问题二:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
问题分析:
我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排.
用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有6个0,6个1的序列,就对应一种方案.
比如000000111111就对应着
第一排:0 1 2 3 4 5
第二排:6 7 8 9 10 11
010101010101就对应着
第一排:0 2 4 6 8 10
第二排:1 3 5 7 9 11
问题转换为,这样的满足条件的01序列有多少个。
观察规律我们发现1的出现前边必须有一个相应的0对应,所以从左到右的所有序列中0的个数要一直大于1的个数。那这种数列有多少种排列方式呢?
那么我们从左往右扫描,第一次出现1的个数等于0的个数是第k位,那么在此之前,0的个数是大于1的个数的。在此之后,0的个数也是大于1的个数的。所以第k位0和1的个数第一次相等的排列有他们这两部分的个数相称的结果。那么所有的k有多少种,则把它们相加起来,就是最后的排列数。这是一个递归的问题。
即 h(n)=h(0)×h(n-1)+h(1)*h(n-2)+...+h(n-1)*h(0)
其他应用:
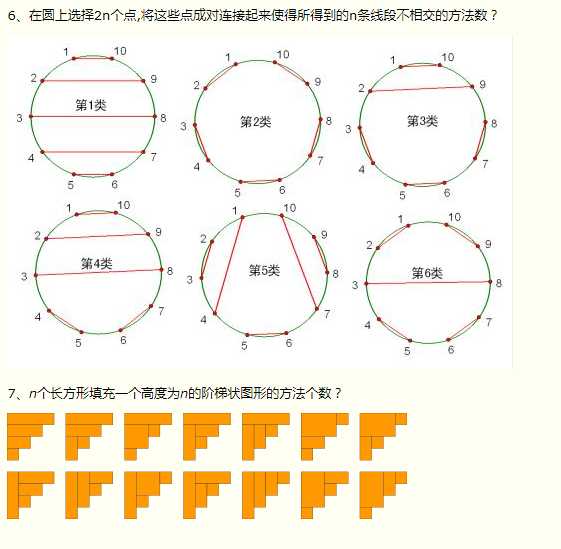
原文:http://www.cnblogs.com/zf-blog/p/7770715.html