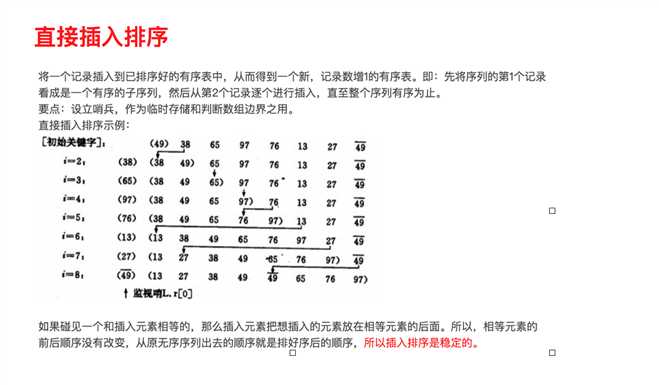
冒泡排序
原始待排序数组| 6 | 2 | 4 | 1 | 5 | 9 |
第一趟排序(外循环)
第一次两两比较6 > 2交换(内循环)
交换前状态| 6 | 2 | 4 | 1 | 5 | 9 |
交换后状态| 2 | 6 | 4 | 1 | 5 | 9 |
第二次两两比较,6 > 4交换
交换前状态| 2 | 6 | 4 | 1 | 5 | 9 |
交换后状态| 2 | 4 | 6 | 1 | 5 | 9 |
第三次两两比较,6 > 1交换
交换前状态| 2 | 4 | 6 | 1 | 5 | 9 |
交换后状态| 2 | 4 | 1 | 6 | 5 | 9 |
第四次两两比较,6 > 5交换
交换前状态| 2 | 4 | 1 | 6 | 5 | 9 |
交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |
第五次两两比较,6 < 9不交换
交换前状态| 2 | 4 | 1 | 5 | 6 | 9 |
交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |
第二趟排序(外循环)
第一次两两比较2 < 4不交换
交换前状态| 2 | 4 | 1 | 5 | 6 | 9 |
交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |
第二次两两比较,4 > 1交换
交换前状态| 2 | 4 | 1 | 5 | 6 | 9 |
交换后状态| 2 | 1 | 4 | 5 | 6 | 9 |
第三次两两比较,4 < 5不交换
交换前状态| 2 | 1 | 4 | 5 | 6 | 9 |
交换后状态| 2 | 1 | 4 | 5 | 6 | 9 |
第四次两两比较,5 < 6不交换
交换前状态| 2 | 1 | 4 | 5 | 6 | 9 |
交换后状态| 2 | 1 | 4 | 5 | 6 | 9 |
第三趟排序(外循环)
第一次两两比较2 > 1交换
交换后状态| 2 | 1 | 4 | 5 | 6 | 9 |
交换后状态| 1 | 2 | 4 | 5 | 6 | 9 |
第二次两两比较,2 < 4不交换
交换后状态| 1 | 2 | 4 | 5 | 6 | 9 |
交换后状态| 1 | 2 | 4 | 5 | 6 | 9 |
第三次两两比较,4 < 5不交换
交换后状态| 1 | 2 | 4 | 5 | 6 | 9 |
交换后状态| 1 | 2 | 4 | 5 | 6 | 9 |
第四趟排序(外循环)无交换
第五趟排序(外循环)无交换
排序完毕,输出最终结果1 2 4 5 6 9
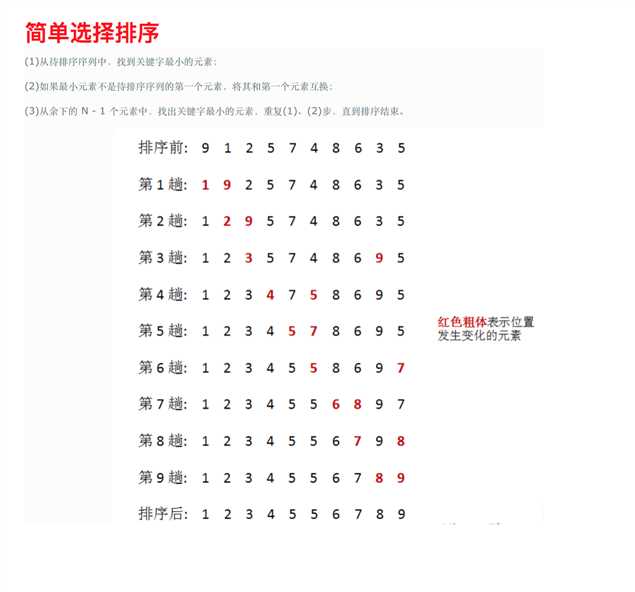

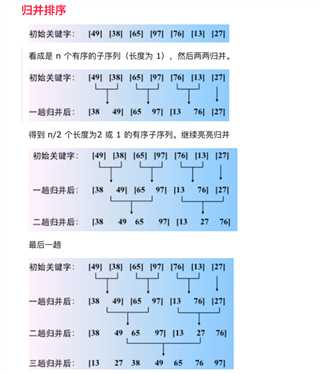


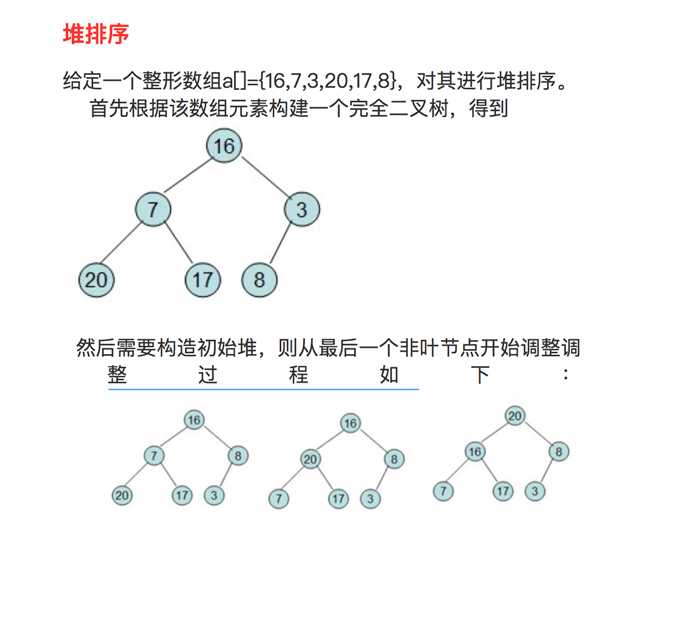
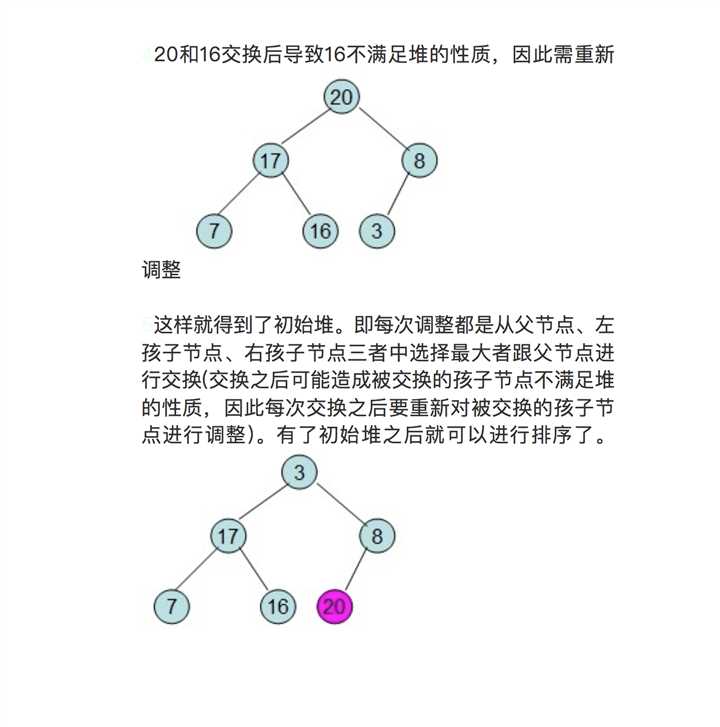
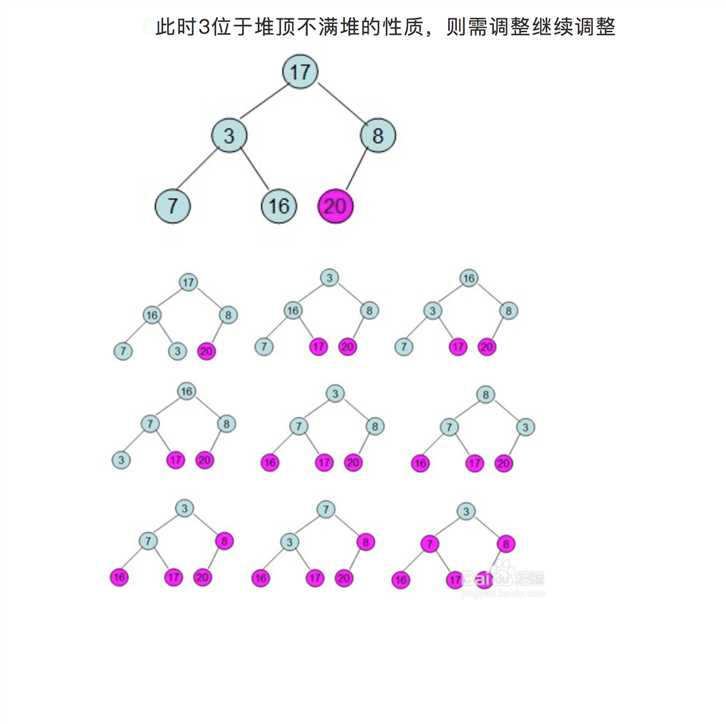
基数排序
1)假设有欲排数据序列如下所示:
73 22 93 43 55 14 28 65 39 81
首先根据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中。
分配结果(逻辑想象)如下图所示:
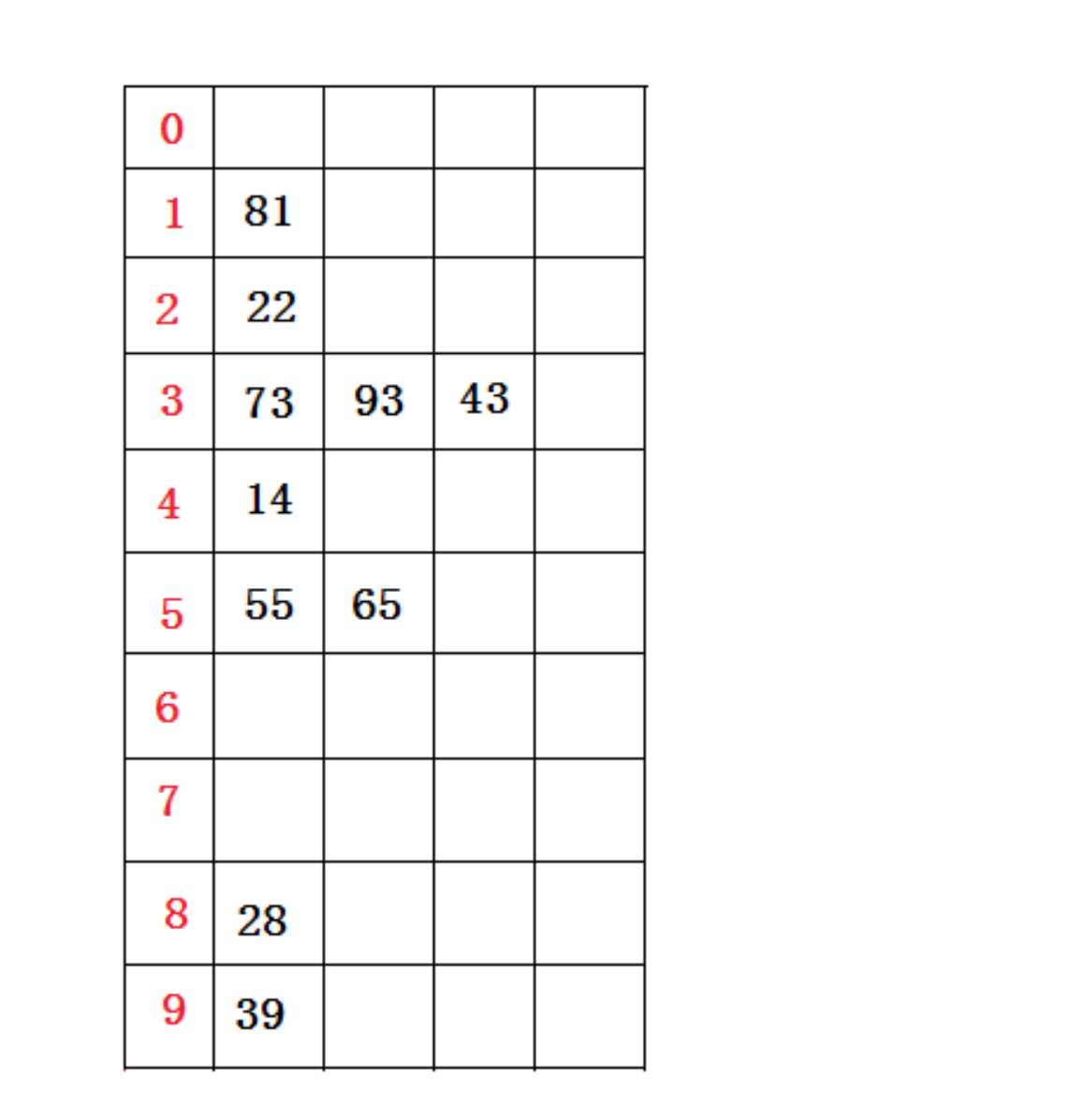
分配结束后。接下来将所有桶中所盛数据按照桶号由小到大(桶中由顶至底)依次重新收集串起来,得到如下仍然无序的数据序列:
81 22 73 93 43 14 55 65 28 39
接着,再进行一次分配,这次根据十位数值来分配(原理同上),分配结果(逻辑想象)如下图所示:
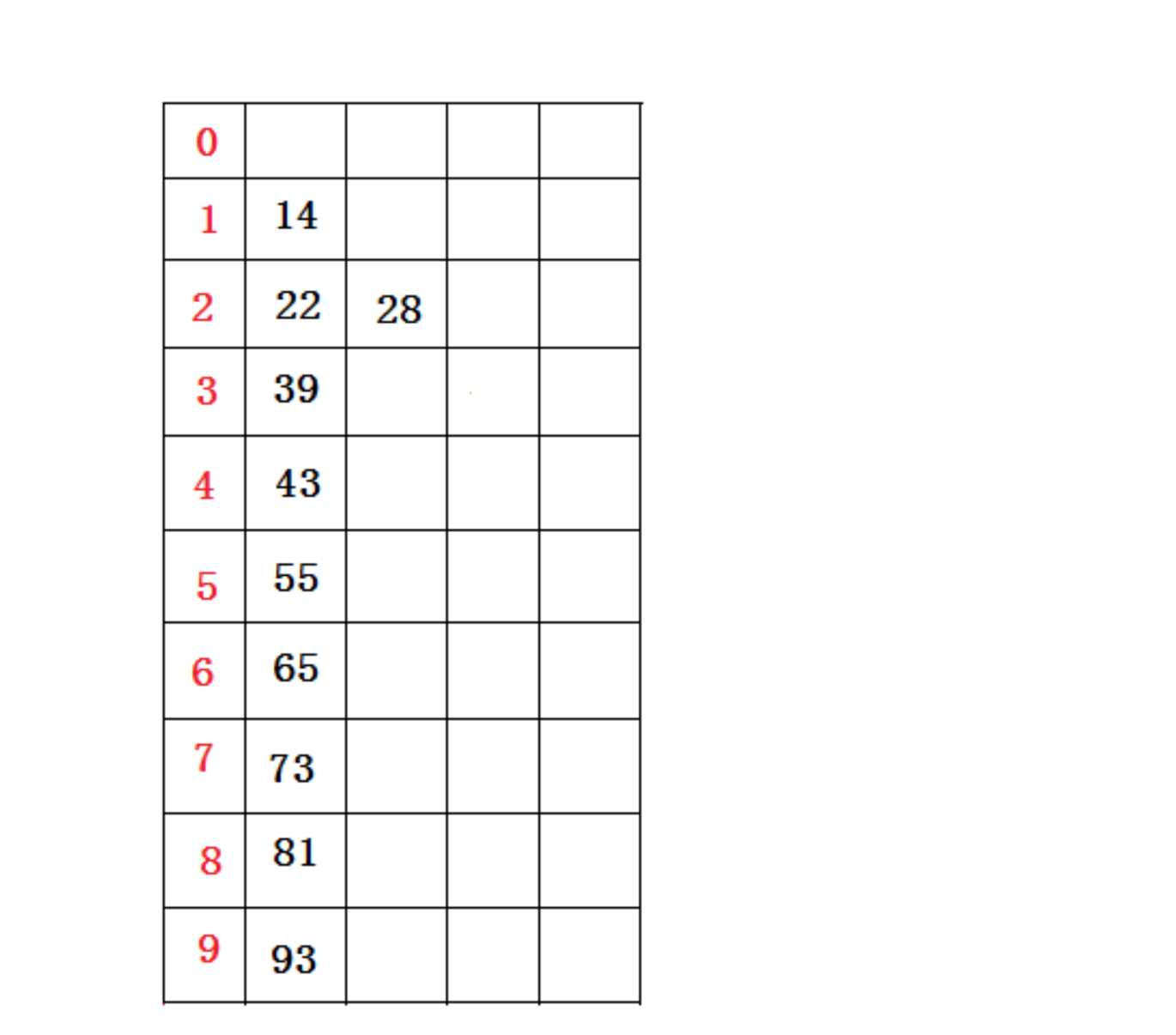
分配结束后。接下来再将所有桶中所盛的数据(原理同上)依次重新收集串接起来,得到如下的数据序列:
14 22 28 39 43 55 65 73 81 93
希尔排序
以n=10的一个数组49, 38, 65, 97, 26, 13, 27, 49, 55, 4为例
第一次 gap = 10 / 2 = 5
49 38 65 97 26 13 27 49 55 4
1A 1B
2A 2B
3A 3B
4A 4B
5A 5B
1A,1B,2A,2B等为分组标记,数字相同的表示在同一组,大写字母表示是该组的第几个元素, 每次对同一组的数据进行直接插入排序。即分成了五组(49, 13) (38, 27) (65, 49) (97, 55) (26, 4)这样每组排序后就变成了(13, 49) (27, 38) (49, 65) (55, 97) (4, 26),下同。
第二次 gap = 5 / 2 = 2
排序后
13 27 49 55 4 49 38 65 97 26
1A 1B 1C 1D 1E
2A 2B 2C 2D 2E
第三次 gap = 2 / 2 = 1
4 26 13 27 38 49 49 55 97 65
1A 1B 1C 1D 1E 1F 1G 1H 1I 1J
第四次 gap = 1 / 2 = 0 排序完成得到数组:
4 13 26 27 38 49 49 55 65 97
原文:http://www.cnblogs.com/mryaohuaiyu/p/7787751.html