matlab离散点拟合二维椭圆的时候,主要有两种方法,一种是使用boundary函数拾取边界点,直接拟合,一共五个参数,使用matlab的regress就可以,公式如下:
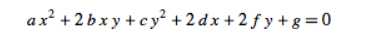
但是这种方法有一些缺点,就是在由于参数过多,拟合垂直情况和系数相差过大的异常椭圆情况会误差会比较大,因此一般使用第二种方法,即将原始的离散点通过使用旋转和平移变化移动到长轴和x轴重合,以原点为中心,最后通过平面变换回去,由于少了b,d,e三项,拟合的精度会好很多,可以解决一些过于扁平的离散点的椭圆拟合,但是这里面会遇到一个很重要的问题就是如何计算旋转角,即通过离散点计算椭圆轴的倾角,由于不是一个一一对应的函数,所以计算起来会有些困难,这里参考http://mathworld.wolfram.com/Ellipse.html的计算方法,公式如下
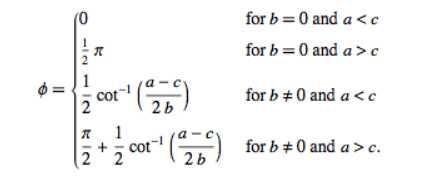
代码如下:
%% 测试验证椭圆形的随机离散方法
% 按照文献中所给算法,但是感觉不准
for anglex=0:pi/90:2*pi
% 常规方法生成
a=20;b=5;
num=400;
x1=-a+2*a*rand(num,1);
y1=-b+2*b*rand(num,1);
xs=[];ys=[];
for i=1:length(x1)
if (x1(i)^2/a^2+y1(i)^2/b^2)<=1
xs=[xs;x1(i)];ys=[ys;y1(i)];
hold on
end
end
plot(xs,ys,‘y*‘);
%% 生成经过平移和旋转的离散点
deltax=3;deltay=6;tx=anglex;
pingyi=[1 0 deltax;0 1 deltay;0 0 1];
xuanzhuan=[cos(tx) -sin(tx) 0;sin(tx) cos(tx) 0;0 0 1]; %逆时针旋转一定的角度
rota_xsys=pingyi*xuanzhuan*[xs‘;ys‘;ones(size(xs‘))];
xs=rota_xsys(1,:);ys=rota_xsys(2,:);
% scatter(x1,y1,‘filled‘);
plot(xs,ys,‘b*‘);
axis equal
hold on
%% 椭圆点边界点拟合--显然更加准确
kp=boundary(xs‘,ys‘,0.1);
xs1=[xs(kp)]‘;ys1=[ys(kp)]‘;
plot(xs1,ys1,‘r‘);
[pxf,~,rp]=regress(-ones(size(xs1)),[xs1.^2 xs1.*ys1 ys1.^2 xs1 ys1]);
a=pxf(1);b=pxf(2);c=pxf(3);d=pxf(4);e=pxf(5);
xc=(b*e-2*c*d)/(4*a*c-b^2);yc=(b*d-2*a*e)/(4*a*c-b^2); %中心
la=sqrt(2*(a*xc^2+c*yc^2+b*xc*yc-1)/(a+c+sqrt((a-c)^2+b^2))); %长半轴
lb=sqrt(2*(a*xc^2+c*yc^2+b*xc*yc-1)/(a+c-sqrt((a-c)^2+b^2))) ;%短半轴
if la<=lb
lx=la;
la=lb;
lb=lx;
end
theta=linspace(0,2*pi,100);
xb=la*sin(theta);yb=lb*cos(theta);
plot(xb,yb,‘g*‘);
%% 求椭圆的倾角
if b==0 && abs(a)<abs(c)
rota=0;
disp([‘角度1=‘ num2str(rota)])
elseif b==0 && abs(a)>abs(c)
rota=pi/2;
disp([‘角度2=‘ num2str(rota)])
elseif b~=0 && abs(a)<abs(c)
ex=1/2*acot((a-c)/b);
rota=ex;
rotax=rota*180/pi;
disp([‘角度3=‘ num2str(rotax)])
elseif b~=0 && abs(a)>abs(c)
ex=1/2*acot((a-c)/b);
rota=pi/2+ex;
rotax=rota*180/pi;
disp([‘角度4=‘ num2str(rotax)])
end
% disp([‘角度‘ num2str(rotax)])
xuanzhuan=[cos(rota) -sin(rota) 0;sin(rota) cos(rota) 0;0 0 1];
pingyi=[1 0 xc;0 1 yc;0 0 1];
rota_xy=pingyi*xuanzhuan*[xb; yb;ones(size(xb))];
% rota_xy=[xc 1;1 yc]*[cos(rota) sin(rota);-sin(rota) cos(rota)]*[xb;yb]; %旋转平移过去
xf1=rota_xy(1,:);yf1=rota_xy(2,:);
% zf1=(df-af.*xf1-bf.*yf1)./cf;
% fs=[xf1‘ yf1‘ zf1‘];
hold on
plot(xf1,yf1,‘k-‘);
title([‘角度=‘ num2str(anglex*180/pi)]);
pause(1);
drawnow
clf
end
测试了360个角度的计算,拟合的椭圆和离散点符合地都比较好。
原文:http://www.cnblogs.com/btlzy2015/p/7858090.html