Notch filter compensates for resonance
Resonance has a pair of complex poles with a real part
The larger the real part - The more the resonance attenuation (complex poles far away imaginary axis)
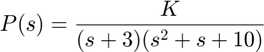
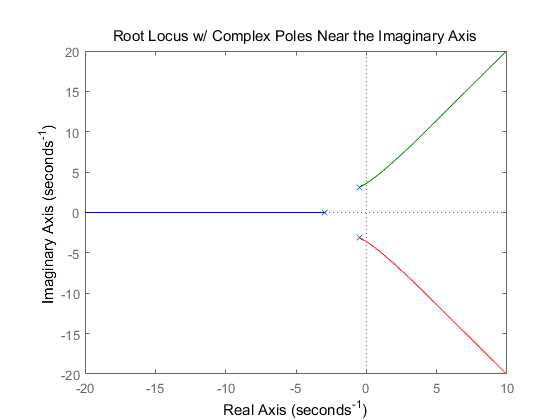
as you can see, the plot shows that this system is only stable for a small region of the root locus(range of gains K). The portion that is stable will be only lightly damped (small ζ).
By closing the loop and plotting the step response for this system in the portion of the root locus that is in the left-half plane(for a gain of one), you can see that the response is poor.
Notch cancels the poles by placing zeros on top of them.
Notch creates different poles with large real part.
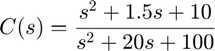
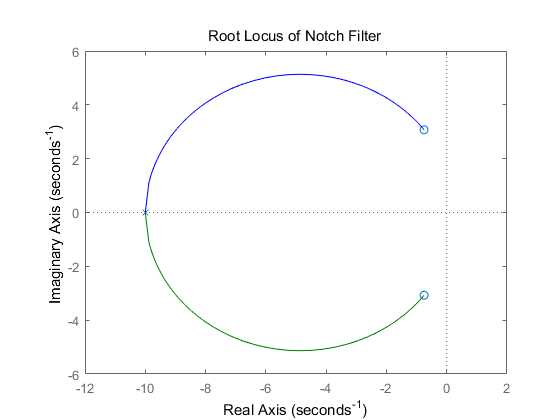
As you can see, the roots of the numerator of the controller are almost the same complex poles of the denominator of the plant; the denominator of the controller introduces two poles at -10.
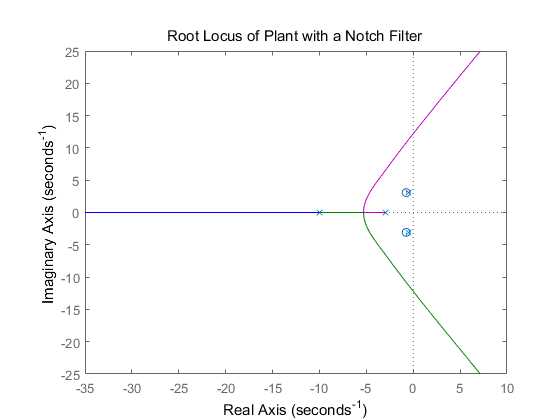
The complex poles near the imaginary axis have been nearly conceled and more of the root locus is now in the left half plane, This means that a larger gain, K, can be employed, while maintaining stability. Furthermore, higher damping ratio can be achieved using lower gains (ζ term wil be larger).
Servo motor control systems with resonance often create difficult problems for designers because it causes the servo control system to over-shoot and oscillate.
An effecitive way to compensate for resonance in a servo system is the use of a notch filter in addition to the standard PID servo loop compensation. To understand the operation of a notch filter, note that every resonance is characterized by two parameters: the imaginary and the real part. The imaginary part sets the resonance frequency. whereas the real part sets the damping. The smaller the real part, the stronger the effect of the resonance.
A notch fiter replaces one resonance with another. It places an anti-resonance on top of the existing resonance, and adds another resonance in a different location. For example, suppose the resonance has a frequency of 100Hz and a real part of 5. The notch cancels this resonance and replaces it by one with a real part of 40. The increase in the real part results in a damped resonance.
The mathematical behavior of the resonance is described by a pair of complex poles in the transfer function. The anti-resonance effect is done by a pair of complex zeros. The notch filter includes a pair of zeros to cancel the resonance and a pair of poles to set the new resonance.
source from courseware of university of moratuwa,
Control Tutorials for MATLAB & SIMULINK - Extras: Notch Filter
Galil motion - using Notch Filters to Compensate for Resonance is Servo Motor Control Systems
原文:http://www.cnblogs.com/zhanghankui/p/7872467.html