题目链接
http://poj.org/problem?id=2492
题意
虫子有两种性别,有n只虫子,编号1~n,输入m组数据,每组数据包含a、b两只虫子,表示a、b为不同性别的虫子,根据输入的m组数据是否出现前后矛盾(如a、b在前面判断为同性,而后又得出a、b为异性)进行相应的输出。
思路
使用并查集求解,但该题比普通并查集题目复杂了一些,该题需要使用树中结点的权值来记录信息,在代码中使用数组r[]来记录某结点和其父结点之间的性别是否相同,若r[x]=0,则说明虫子x和其父结点同性,若r[x]=1,则说明x与其父结点异性,这也是“带权”的含义。
代码
1 #include <cstdio> 2 3 const int N = 2000 + 10; 4 int p[N]; 5 int r[N]; 6 7 void make_set(int n) 8 { 9 for (int i = 1;i <= n;i++) 10 { 11 p[i] = -1; 12 r[i] = 0; 13 } 14 } 15 16 int find_root(int x) 17 { 18 if (p[x] == -1) return x; 19 20 int t = p[x]; 21 p[x] = find_root(p[x]); 22 r[x] = (r[x] + r[t]) % 2; 23 return p[x]; 24 } 25 26 void union_set(int a, int b) 27 { 28 int ra = find_root(a); 29 int rb = find_root(b); 30 31 p[ra] = rb; 32 r[ra] = (r[a] + r[b] + 1) % 2; 33 } 34 35 int main() 36 { 37 //freopen("poj2492.txt", "r", stdin); 38 int t; 39 scanf("%d", &t); 40 int cnt = 0; 41 while (t--) 42 { 43 int n, m; 44 scanf("%d%d", &n, &m); 45 make_set(n); 46 bool flag = true; 47 int a, b; 48 for (int i = 0; i < m; i++) 49 { 50 scanf("%d%d", &a, &b); 51 if (find_root(a) == find_root(b)) 52 { 53 if (r[a] == r[b]) 54 { 55 flag = false; 56 continue; 57 } 58 } 59 else union_set(a, b); 60 } 61 printf("Scenario #%d:\n", ++cnt); 62 if (flag) 63 puts("No suspicious bugs found!\n"); 64 else puts("Suspicious bugs found!\n"); 65 } 66 return 0; 67 }
分析
第一次做带权并查集,下面是我对代码的一些分析:
1、首先要注意函数int find_root(int x)。函数find_root不仅进行了路径压缩,而且还更新了结点和其父结点之间的关系,更新后的关系r[x]=(r[x]+r[t])%2,其中t为x的父结点。为什么是r[x]=(r[x]+r[t])%2呢?首先要知道路径压缩后树变成了2层,每个结点直接与根结点相连,假设有3只虫子a、b、c,关系如下
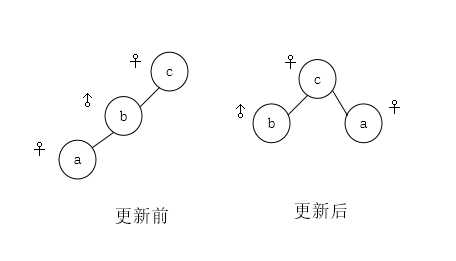
则更新前有r[a]=1,r[b]=1,更新后r[a]=0=(r[a]+r[b])%2,考虑全部情况,则可以得到下表:
| 更新前r[a] | r[b] | 更新后r[a] |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
可以看到有r[a]=(r[a]+r[b])%2(其实就是把更新前r[a]和r[b]做了一次异或操作得到新的r[a],写成r[a]=r[a]^r[b]也可以)。
2、还要注意函数union_set中为什么会有r[ra]=(r[a]+r[b]+1)%2?分析方法和上面是相同的,把r[a]、r[b]、r[ra]的值列举出来就可以发现r[ra]=(r[a]+r[b]+1)%2
相似题目
1、poj1703
原文:http://www.cnblogs.com/sench/p/7944239.html