[知识点]莫比乌斯反演入门

因为今天有较为充足的时间，于是果断入坑反演OvO

直接上公式和概念：

定理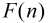：和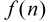是定义在非负整数集合上的两个函数，并且满足条件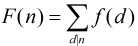，那么我们得到结论

在上面的公式中有一个函数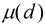，称其为莫比乌斯函数

它的定义如下：

    （1）若，那么

    （2）若，均为互异素数，那么

    （3）其它情况下

对于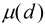函数，它有如下的常见性质：

    （1）对任意正整数有              

 　　

   （2）对任意正整数有

　　

   （3）为积性函数

　　数论上积性函数的定义：

　   

　　积性函数的性质：
　　① 

　　②积性函数的前缀和也是积性函数

由此可以线性求出莫比乌斯函数：

    mu[1]=1;notprime[1]=1;
    pos(i,2,N-10){
        if(!notprime[i]){
            mu[i]=-1;
            prime[++prime[0]]=i;
        }
        for(int j=1;j<=prime[0]&&prime[j]*i<=N-10;j++){
            notprime[i*prime[j]]=1;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }　　

莫比乌斯反演一般描述为

但是我们做题一般是用到

来几道入门题感受一下：

[BZOJ 2301]Problem B 题解　　

[BZOJ 2820]YY的GCD     

[知识点]莫比乌斯反演入门

原文：http://www.cnblogs.com/Hallmeow/p/7994506.html