简单入门一下矩阵树Matrix-Tree定理。(本篇目不涉及矩阵树相关证明)
一些定义与定理
- 对于一个无向图 G ，它的生成树个数等于其基尔霍夫Kirchhoff矩阵任何一个N-1阶主子式的行列式的绝对值。
- 所谓的N-1阶主子式就是对于一个任意的一个 r ，将矩阵的第 r 行和第 r 列同时删去得到的新矩阵。
- 基尔霍夫Kirchhoff矩阵的一种求法：
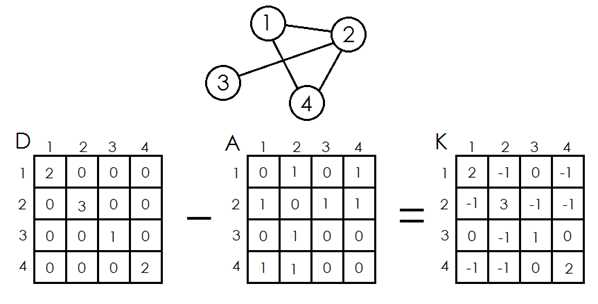
基尔霍夫Kirchhoff矩阵 K =度数矩阵 D - 邻接矩阵 A
基尔霍夫Kirchhoff矩阵的具体构造
- 度数矩阵D：是一个 ${N}\times{N}$ 的矩阵，其中
$D[i][j]=0\;{(i}\neq{j)}$，$D[i][i]=i号点的度数$
- 邻接矩阵A：是一个 ${N}\times{N}$ 的矩阵，其中
${D[i][i]=0}\;{,}\;{A[i][j]=A[j][i]=i,j之间的边数}$
- 然后基尔霍夫Kirchhoff矩阵K=D-A
- 举个例子，对于如下的无向图，三个矩阵分别为
行列式det(K)求法
- 已经得出了基尔霍夫Kirchhoff矩阵，那么随便去掉某一行一列并计算出新矩阵的行列式，其绝对值即为生成树个数。
- ${det(K)=}\sum_{P}^{ }\;{(}{(-1)}^{\tau{(P)}}\times{K}_{1,p1}\times{K}_{2,p2}\times{K}_{3,p3}\times\cdots\times{K}_{N,pN}{)}$
- 上面的式子中的 P 为 1~N 的任意一个排列。$\tau{(P)}$表示排列 P 的逆序对数。而那个求和式的每一项可以看做是在矩阵中选出N个数，使得他们的行列都不重合。
- 求和式共有$N!$项，暴力求法的复杂度 ${O(N!)}\times{N}$
1
1
1
1
1
1