emmmm,这东西看了我一天多,终于有一个大概的概念了
红黑树是一种特殊的二叉搜索树
它可以保证,无论以什么样的顺序进行插入和删除,二叉搜索树的树高均为lg(n)
首先红黑树继承了所有二叉搜索树的性质
红黑树接着还有另外五个性质,这些性质满足了树高为lg(n)的特性
除了树中的节点,我们会在每个叶子节点后加两个黑色的空节点
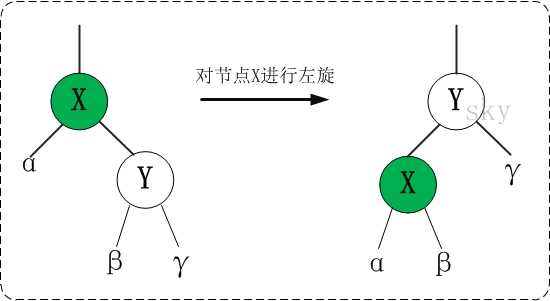
旋转:
对于节点x的左旋就是把x与x的左儿子互换位置,并保证二叉搜索树的性质不变
右旋同理
插入:
首先,按二叉搜索树的方法进行插入
然后把插入的节点涂成红色
接着通过一系列染色,旋转等操作保证这棵树满足红黑树的性质
删除:
首先,按二叉搜索树的方法进行删除
我们知道,删除有三种情况
若x为根节点直接删除,此时无论x为红或黑,均不影响性质
若x有一支,若x为红,无影响,否则此支的黑高会少一
若x有两支,我们找到该替换他的那一个y然后用y的值代替x的值,并删除y
那么第三种情况就转换为前两种情况了
在删除之后,我们在通过一系列操作来使这棵树的性质恢复
可以看见,无论是插入还是删除,我们都是对红黑树的叶子节点,或者只有一支的节点进行操作的
也就是说在树的下面进行操作
想一下,对于一个二插搜索树,我要尽量保证每一个节点的两边节点数量均衡
我们仔细的看下左旋的右旋的图片
如果x是根节点
那么左旋的话左子树的高度+1,右子树的高度-1
啧啧,是不是有点看明白了
对于插入和删除我通过红黑树的操作不断地把异常节点上移,最后通过对根节点的操作调节左右子树的高度,搞定
ps: 发明红黑树的这人一定是个天才