原文链接http://www.cnblogs.com/zhouzhendong/p/8111725.html
题目传送门 - BZOJ3560
题意概括
给定n个正整数a1,a2,…,an,求
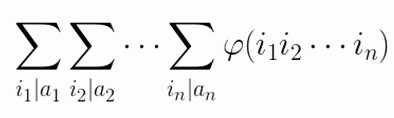
的值(答案模10^9+7)。
1<=n<=10^5,1<=ai<=10^7。
题解
本人是蒟蒻。
可以看这位大佬的(给出链接)
http://blog.csdn.net/popoqqq/article/details/42739963
代码
呵呵,调试的时候照着他的改,改的几乎一样……
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const LL N=100005;
LL mod=1e9+7;
LL n,tot=0;
struct Node{
LL p,t;
}q[N*20];
bool operator < (Node a,Node b){
return a.p<b.p;
}
void fj(LL v){
for (LL i=2;i*i<=v;i++)
if (v%i==0){
q[++tot].p=i;
q[tot].t=0;
while (v%i==0)
v/=i,q[tot].t++;
}
if (v>1)
q[++tot].p=v,q[tot].t=1;
}
LL Pow(LL x,LL y,LL mod){
if (y==0)
return 1LL;
LL xx=Pow(x,y/2,mod);
xx=xx*xx%mod;
if (y&1LL)
xx=xx*x%mod;
return xx;
}
LL Inv(LL x,LL mod){
return Pow(x,mod-2,mod);
}
LL calc(LL L,LL R){
LL sum[30];
LL p=q[L].p,res=1;
sum[0]=1;
for (int i=1;i<30;i++)
sum[i]=(sum[i-1]*p+1)%mod;
for (int i=L;i<=R;i++)
res=res*sum[q[i].t]%mod;
res=(res-1)*(p-1)%mod*Inv(p,mod)%mod+1;
return res%mod;
}
int main(){
scanf("%lld",&n);
for (int i=1,a;i<=n;i++){
scanf("%lld",&a);
fj(a);
}
sort(q+1,q+tot+1);
int last=0;
LL ans=1;
for (int i=1;i<=tot;i++)
if (i==tot||q[i].p!=q[i+1].p)
ans=ans*calc(last+1,i)%mod,last=i;
printf("%lld",(ans%mod+mod)%mod);
return 0;
}
