Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 672 Accepted Submission(s): 116
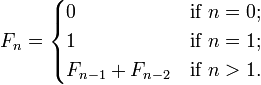That is, after two starting values, each number is the sum of the two preceding numbers. The first Fibonacci numbers (sequence A000045 in OEIS), also denoted as F[n]; F[n] can be calculate exactly by the following two expressions: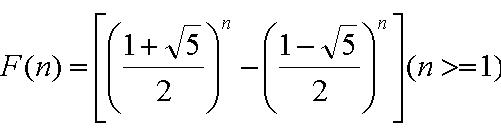 
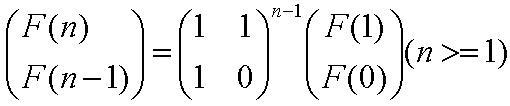A Fibonacci spiral created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;
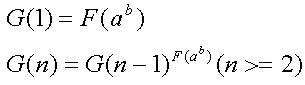Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod CIn mathematics, Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers of the following integer sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
By definition, the first two numbers in the Fibonacci sequence are 1 and 1, and each subsequent number is the sum of the previous two. In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation Fn = Fn - 1 + Fn - 2 with seed values F1 = 1 and F2 = 1.
And your task is to find ΣFiK, the sum of the K-th power of the first N terms in the Fibonacci sequence. Because the answer can be very large, you should output the remainder of the answer divided by 1000000009.
There are multiple test cases. The first line of input is an integer T indicates the number of test cases. For each test case:
There are two integers N and K (0 <= N <= 1018, 1 <= K <= 100000).
For each test case, output the remainder of the answer divided by 1000000009.
5 10 1 4 20 20 2 9999 99 987654321987654321 98765
143 487832952 74049690 113297124 108672406
The first test case, 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143.
The second test case, 120 + 120 + 220 + 320 =3487832979, and 3487832979 = 3 * 1000000009 + 487832952, so the output is 487832952.
2 5 5 13 5
0 3
2014年蓝桥杯的第九题是这样描述的：
给定Fibonacci数列F[]，其中
的值。其中
喵喵因为太弱，没有进Final，终身遗憾。她就挂在了这个题目上。
已知：
F0 = 1 , F1 = 1 , F2 = 2 , Fn = Fn-1+Fn-2
求：
FFFn Mod P
( 也就是 F[ F[ F[n] ] ] % P )
第一行一个整数 T 代表数据组数(T ≤ 20000)。 <del> 
喵以人格担保时限肯定够！！！</del>
以下每行两个整数 N , P (0 ≤ N ≤ 109 , 1 ≤ P ≤ 109)
4 1 2 2 3 4 35 4 31
1 2 34 3
F1 = 1 , F1 = 1 , F1 = 1
F2 = 2 , F2 = 2 , F2 = 2
F4 = 5 , F5 = 8 , F8 = 34
八个用空格隔开的整数n, m, a, b, c, d, e, f，其中n, m, a, b, d, e为正整数，c, f为非负整数。
一个整数，表示Fib[n][m]对2012182013取模的值。
n,m,a,b,c,d,e,f<=10^1000000
题目：http://codeforces.com/contest/392/problem/C
题意：给定Fibonacci数列F[]，令
今天将来学习如何求广义Fibonacci数列的循环节。
问题：给定
环节长度。
来源：http://acdreamoj.sinaapp.com/ 1075题
2 4 5
6 20
2 5 5 13 5
0 3
100
F(100)= 3 * 5^2 * 11 * 41 * 101 * 151 * 401 * 3001 * 570601
6 ba
3
原文：http://www.cnblogs.com/HaibaraAi/p/3825349.html