后缀自动机,一个处理字符串问题的神器。听起来很神圣,貌似很难写。其实代码实现并不复杂,萌新估计都能学会。
以前听学长们讲过好多次也看过陈立杰的课件,都不是很明白。今天终于弄明白了,就写一个让大家都能看懂的讲解(其实主要是给自己复习用的QAQ),来填坑吧。
学习这种东西最好用笔在草稿纸上多画一画,遇到不懂得尝试举例看一看,就直观多了。
首先先明确几个定义:
·对于字符串S,他的后缀自动机为SAM。
·初始位置为init。
·如果自动机无法识别当前串,则会转移到Null(空);并且规定Null只能转移到Null。
·规定trans(s,ch)为当前状态为s,读入ch后转移到的状态
·规定Reg(A)为自动机能识别的串的集合。即使得trans(init,x)∈end的串x。
·规定Reg(s)为从s开始能识别的串的集合,即使得trans(init,sx)属于Reg(A)的x的集合。
·规定SAM(x)=1,当且仅当x是S的后缀,SAM(x)≠Null,当且仅当x是S的后缀或子串。
·ST(str)表示trans(init,str),即从初始状态转移str后达到的状态。
·规定母串S的后缀集合为Suf,连续子串集合为Fac,从位置a开始的后缀为Suffix(a)。
·规定S[l,r)表示S区间[l,r)的子串(前闭后开),下标从0开始。
然后,我们可以得到一些推论:
若串s?Fac,则ST(s)=Null。
我们考虑ST(a)之后能接那些字符串,即Reg(ST(a)),ST(a)能识别S,当且仅当ax是S的后缀。所以,x也是s的后缀。Reg(ST(a))是后缀的一个集合。
画出来是这样的:
对于一个状态,我们只关心Reg(x)。
若字符串a在原串S的[l,r)出现,则可以识别S从r开始的的后缀。
设a在[l1,r1),[l2,r2)...[ln,rn)中出现,则Reg(ST(a))为{suffix(r1),suffix(r2)...suffi(rn)}。
设Right(a)={r1,r2...rn},则Reg(ST(a))完全由right(a)决定(这不是显然吗,但是注意right()并不决定a,之后会讲)。
那么,若right(a)=right(b),则两个状态可结束的右区间相同,那么ST(a)=ST(b)。
故一个状态s(或者叫串的集合s),由所有right(x)相同均为right的串x组成。
设r∈right(s),则在给定长度len后可以唯一确定该子串为s[ri-len,ri),其中ri为集合任意一个r(为什么左边是减,右边不动?区间左边小)。
考虑下面的串:
若让集合right(s)包含且仅包含5,11(即蓝色),那么s可为的子串为:aaaab,aaab,其长度为4,5。
若让集合right(s)包含且仅包含5,11,17,22(即蓝色和红色),那么s可为的子串为:aab,ab,其长度为2,3。
所以,对于一个集合right(s),其s的长度是一个区间,我们定义这个区间为[min(s),max(s)]。
证明:如果长度l,r合适,则l,r之间的所有长度均合适(这个显然)。如果长度为r+1,则会扩大限制,缩小集合(上面例子中第二个集合变成第一个);若长度为l-1,则会松弛限制,扩大集合(上面例子中第一个到第二个)。(感觉我讲的已经很明白了吧QAQ)
状态数为线性的证明:
点数线性:
考虑两个状态a、b,其right集合分别为Ra,Rb。
假设Ra,Rb存在交集,即有r包含于Ra且r包含于Rb(原谅我真的打不出符号了)。
a、b表示的子串不会有交集(为什么?否则他们不是两个状态。对于某个串str,ST(sta)既为a又为b,那么a、b就是同一个状态了的说)。
因为字符串无交集而r有交集,那么对于r中的位置。其表示的前置字符串长度不同。
所以,就有:
我们不妨设(钦定)minB>maxA,这样的话,a中所有的串均为b中所有的串的后缀。对于所有Right(B)中的位置r,其前面a中所有的串一定都出现了。而a对长度的限制更小,所以集合Ra一定比集合Rb大。故Rb为Ra的真子集。(这里讲的和陈立杰课件不一样,严重怀疑其幻灯片有错)
所以,我们证明了:对于两个Right集合,要么完全不相交,要么一个是另一个的真子集。
这样的话我们可以把他们画成一棵树:
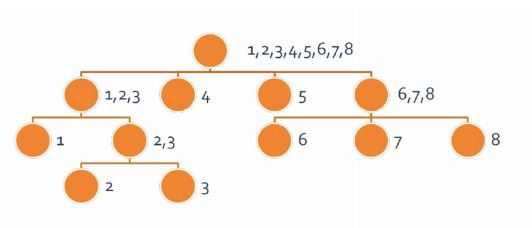
(借用陈立杰课件的图)
我们称之为parent树。
这棵树上叶子节点数量为O(n)的,而非叶子节点每个节点最少两个子树(什么你说一个?为什么不合并了它),数量也是O(n)的。故节点个数为O(n)的。所以节点个数是线性的。
另外,对于下面的s,如果选的串比min(s)更短,则会跑到其父亲一层去。所以,max(fa)=min(s)-1。
边数线性:
对于一条由状态a开始,字符为c的边,如果Trans(a,c)为Null,我们可以不存储它。
而如果Trans(a,c)=b(ab为状态),那么则有一条a->b的标号为c的边。
我们先求出一个SAM的生成树,生成树的边数为O(n)的。
我们考虑一个非树边,如果有状态通过他转移,那么则有init经过“生成树状态中a + 非树边a->b + 生成树状态b”到一个ed。
这是一条init->ed的路径,为一个后缀。
我们另一个后缀对应第一个非树边,那么一个后缀最多对应一条非树边(显然),一个非树边至少被一个后缀对应(这个为什么?)。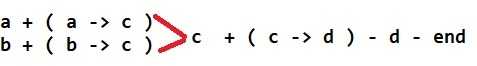
其中所有小括号表示非树边。
那么由于c->d只会被“跨过”,那么我们可以把状态cd合并掉也没关系吧,换句话说,状态c没有存在的必要,状态c和d本来就应该是一个状态!
由于后缀数量是O(n)的,所以非树边数量也是O(n)的,总体还是O(n)的。这样也就证明了边数是线性的。
如何存储:
我们显然不能在一个状态中存储所有right集合。因为我们不知道一个位置会被存储多少次,这样会MLE。
然而一个状态的right集合一定是其后代叶子节点的并集。
按照DFS序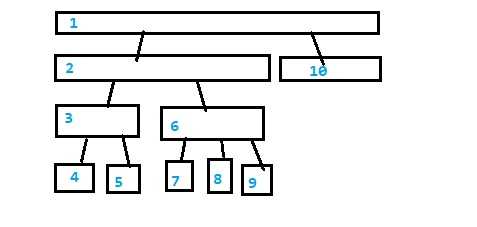
对于上面节点的right集合,一定是DFS序上连续的一段区间。(为什么?DFS序保证子树为连续区间的说)
对于状态s,其right集合为right(s),若有s->t,字符为c的边,则在s的right中,只有S[ri]==c的符合要求,那么t的right集合为{ri+1|r[i]==c},且max(t)>max(s)(为什么?多了一个字符c的说)。
如果s出发有字符为x的边,那么parent(s)出发的也有(为什么,因为parent(s)表示s的后缀!)。令f=parent(s),则right(trans(s,c))包含于right(trans(f,c))。
实现:
可能你感觉我说了这么多废话证明,这玩意到底怎么写呢?
好,下面讲一下怎么实现。
一开始我们有一个空的SAM,现在考虑如何增加一位,即把字符串T的SAM拓展为字符串Tx的SAM。
令p=ST(T)(说白了就是上次加入的节点QAQ),新建np=ST(Tx)。连接trans(p,x)=np。
对p无转移x的祖先v,令trans(v,x)=np。
找到p第一个有转移x的祖先vp。如果没有vp,令parent(np)=root,拓展结束,返回。
令q=trans(vp,x),若max(q)==max(vp+1),直接令parent(np)=q,拓展结束,返回(这种情况表示np为q的子集,同时直接加入不会使max(q)变得更小,所以直接连接就可以了。举个例子的话,q表示ab,np表示aab,vp表示a。)。
否则新建节点nq,使得trans(nq,*)=trans(q,*),parent(nq)=parent(q),max(nq)=max(vp)+1,然后让parent(np)=parent(q)=nq(这种情况表示nq的串比vp+1长,强行插入会使之max变小,所以加入一个更短的节点并把后继拆成两个独立的节点。例如vp表示a,q表示aaab,np表示aab,这样强行插入会使得q的max变小。而这两种状态都是状态ab的子集,所以我们新建nq表示ab即可)。
最后上代码:

1 struct Node { 2 int mx; 3 Node *par,*nxt[26]; 4 }ns[maxn],*root,*last; 5 6 inline Node* NewNode(int len) { 7 static int cnt = 0; 8 ns[++cnt].mx = len; 9 return &ns[cnt]; 10 } 11 12 inline void extend(int x) { 13 Node *p = last; 14 Node *np = NewNode(p->mx+1); 15 while( p && !p->nxt[x] ) 16 p->nxt[x] = np, 17 p = p->par; 18 if( !p ) 19 np->par = root; 20 else { 21 Node* q = p->nxt[x]; 22 if( q->mx == p->mx + 1 ) 23 np->par = q; 24 else { 25 Node* nq =NewNode(p->mx+1); 26 memcpy(nq->nxt,q->nxt,sizeof(q->nxt)); 27 nq->par = q->par; 28 q->par = np->par = nq; 29 while( p && p->nxt[x] == q ) 30 p->nxt[x] = nq, 31 p = p->par; 32 } 33 } 34 last = np; 35 }
例题:
SPOJ NSUBSTR:
一句话题面:给定一个字符串,求每个对应的长度能产生的相同子串的最大个数。
相同子串个数就是其后缀自动机节点上right()集合的大小,并且长的字符串可以切割成短的,所以我们只用每个节点可表示的最长长度去更新即可。
我们先构建出后缀自动机,然后再parent树上反向拓扑排序跑出right大小,更新答案。然后把答案倒着扫一遍用长的更新短的即可。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #define debug cout 7 using namespace std; 8 const int maxn=5e5+1e2; 9 10 char in[maxn]; 11 int f[maxn],len,cnt; 12 13 struct Node { 14 int mx; 15 Node *par,*nxt[26]; 16 int right,deg; 17 }ns[maxn],*root,*last; 18 19 inline Node* NewNode(int len) { 20 ns[++cnt].mx = len; 21 return &ns[cnt]; 22 } 23 24 inline void extend(int x) { 25 Node *p = last; 26 Node *np = NewNode(p->mx+1); 27 np->right = 1; 28 while( p && !p->nxt[x] ) 29 p->nxt[x] = np, 30 p = p->par; 31 if( !p ) 32 np->par = root; 33 else { 34 Node* q = p->nxt[x]; 35 if( q->mx == p->mx + 1 ) 36 np->par = q; 37 else { 38 Node* nq =NewNode(p->mx+1); 39 memcpy(nq->nxt,q->nxt,sizeof(q->nxt)); 40 nq->par = q->par; 41 q->par = np->par = nq; 42 while( p && p->nxt[x] == q ) 43 p->nxt[x] = nq, 44 p = p->par; 45 } 46 } 47 last = np; 48 } 49 50 inline void topo() { 51 queue<int> q; 52 for(int i=1;i<=cnt;i++) 53 if( &ns[i] != root ) 54 ++ns[i].par->deg; 55 for(int i=1;i<=cnt;i++) 56 if( !ns[i].deg ) 57 q.push(i); 58 while( q.size() ) { 59 const int pos = q.front(); q.pop(); 60 if( &ns[pos] == root ) 61 break; 62 ns[pos].par->right += ns[pos].right; 63 f[ns[pos].mx] = max( f[ns[pos].mx] , ns[pos].right ); 64 --ns[pos].par->deg; 65 if( !ns[pos].par->deg ) 66 q.push( ns[pos].par - ns ); 67 } 68 } 69 70 inline void calc() { 71 for(int i=len-1;i;i--) 72 f[i] = max( f[i] , f[i+1] ); 73 } 74 75 int main() { 76 scanf("%s",in+1); 77 len = strlen(in+1); 78 79 last = root = NewNode(0); 80 for(int i=1;i<=len;i++) 81 extend(in[i]-‘a‘); 82 83 topo(); 84 calc(); 85 86 for(int i=1;i<=len;i++) 87 printf("%d\n",f[i]); 88 89 return 0; 90 }
SPOJ SUBLEX:
一句话题面:对于给出的长度不超过90000的字符串进行Q(Q <= 500)次询问, 每次询问给出一个K, 要求输出第K小的子串(0 < K < 2^31),其中相同的子串只算一次例如“aaa"的子串是"a", "aa", "aaa"
考虑如果在Trie树上怎么做,先统计size然后26分字符。在后缀自动机上也这样做即可。注意到后缀自动机沿着匹配字符边走是一个DAG,所以我们直接用记忆化搜索跑出走这个方向存在表示的字符串个数即可。(这么鬼畜的东西我是拒接写迭代的QAQ)
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=2e5+1e2; 10 11 char in[maxn]; 12 int len,m,cnt; 13 14 struct Node { 15 Node *fa,*fm,*nxt[26]; 16 int len; 17 lli sum; 18 }ns[maxn],*root,*last; 19 20 inline Node* NewNode(int ll) { 21 ns[++cnt].len = ll; 22 return &ns[cnt]; 23 } 24 25 inline void extend(int x) { 26 Node* p = last; 27 Node* np = NewNode(p->len+1); 28 while( p && !p->nxt[x] ) 29 p->nxt[x] = np, 30 p = p->fa; 31 if( !p ) 32 np->fa = root; 33 else { 34 Node* q = p->nxt[x]; 35 if( q->len == p->len + 1 ) 36 np->fa = q; 37 else { 38 Node* nq = NewNode(p->len+1); 39 memcpy(nq->nxt,q->nxt,sizeof(q->nxt)); 40 nq->fa = q->fa; 41 np->fa = q->fa = nq; 42 while( p && p->nxt[x] == q ) 43 p->nxt[x] = nq, 44 p = p->fa; 45 } 46 } 47 last = np; 48 } 49 50 inline lli dfs(Node* pos) { 51 if( pos->sum ) 52 return pos->sum; 53 lli ret = 0; 54 for(int i=0;i<26;i++) 55 if( pos->nxt[i] ) 56 ret += dfs(pos->nxt[i]); 57 pos->sum = ret + ( pos != root ); 58 return pos->sum; 59 } 60 61 inline void query(lli x) { 62 Node* pos = root; 63 while( x ) { 64 for(int i=0;i<26;i++) 65 if( pos->nxt[i] ) { 66 if( x <= pos->nxt[i]->sum ) { 67 putchar(i+‘a‘); 68 pos = pos -> nxt[i]; 69 --x; 70 break; 71 } 72 else 73 x -= pos->nxt[i]->sum; 74 } 75 } 76 putchar(‘\n‘); 77 } 78 79 int main() { 80 scanf("%s",in+1); 81 len = strlen(in+1); 82 83 last = root = NewNode(0); 84 for(int i=1;i<=len;i++) 85 extend(in[i]-‘a‘); 86 87 dfs(root); 88 89 scanf("%d",&m); 90 while( m-- ) { 91 lli x; 92 scanf("%lld",&x); 93 query(x); 94 } 95 96 return 0; 97 }
完结撒花!!祝大家元旦快乐2333。

