【自动机】
有限状态自动机的功能是识别字符串，自动机A能识别字符串S，就记为$A(S)$=true，否则$A(S)$=false。
自动机由$alpha$（字符集），$state$（状态集合），$init$（初始状态），$end$（结束状态集合），$trans$（状态转移函数）组成。
令$trans(s,str)$表示当前状态是$s$，读入字符串或字符$str$后达到的状态。
从状态$s$开始能识别的字符串$x$满足$trans(s,x)\subset end$。
【后缀自动机（SAM)】
SAM(suffix automaton)是一个能识别字符串$S$的所有后缀的自动机。
即$SAM(x)=true$，当且仅当$x$是$S$的后缀。
【有限状态后缀自动机】
有限状态后缀自动机是状态数最少的后缀自动机，大小为$O(n)$。
令$ST(a)=trans(init, a)$
如果字符串$a$在$S$中的$[l,r)$中出现，那么它就能识别$S$从$r$开始的后缀。
如果$a$在$S$中出现的位置为$\{[l_1, r_1),[l_2, r_2), ..., [l_n, r_n)\}$，那么$a$能识别的字符串为$\{suffix(r_1), suffix(r_2), ..., suffix(r_n)\}$。
令$right(a)={r_1, r_2, ..., r_n}$，那么$a$能识别的字符串完全由$right(a)$决定，也就是说如果$right(a)=right(b)$，则有$ST(a)=ST(b)$。
所以一个状态$s$，由所有right集合为$right(s)$的字符串组成。
只要给定一个$Right$集合，再给定一个长度，就确定了一个子串。
一个$Right$集合所对应的子串长度是一个区间，换句话说，如果对于一个$Right$集合，若长度$l$和$r$合适，则对于满足$l\leq x \leq r$的长度$x$也合适。因为如果$x$确定的子串$a_x$的某个出现位置不在$Right$集合中，那么$r$确定的子串$a_r$作为$a_x$的后缀，肯定也有某个位置不在$Right$中。如果$Righr$中的某个位置无法确定$a_x$，那么$a_x$作为$a_l$的后缀，也会有某个位置无法确定$a_l$。
于是令$[min(s), max(s)]$表示状态s的长度区间。
【状态数的线性证明】
假设两个状态$a, b$，假设$right(a)$和$right(b)$有交集。
因为$a,b$不同，所以这两个状态表示的子串无交集，$[min(a), max(a)]$和$[min(b), max(b)]$也无交集。因为如果有交集，那么他们的$Right$集合必定相等，就变成同一个状态了。
因为$right(a), right(b)$有交集，设$min(a)>max(b)$，那么$b$表示的所有子串长度都比$a$的小，而右端点相同，也就是说$b$中所有子串都是$a$中子串的后缀。也就是说$a$所出现的所有位置，$b$都出现了，所以$r_a\subset $r_b$，也就是$r_a$是$r_b$的真子集。
也就是说要么两个状态的$Right$集合不相交，要么其中一个状态的$Right$集合是另一个的真子集。
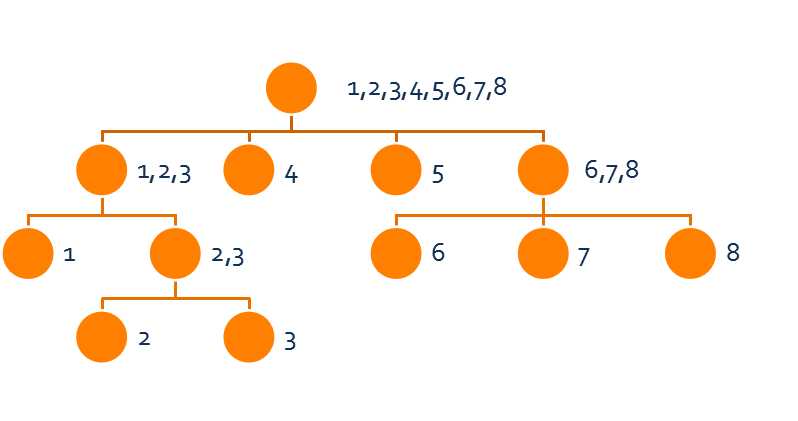
上方是所有状态的$Right$集合的示意图，我们称之为$Parent$树。
在这个树里，每个节点至少有两个儿子，所以节点的个数是$O(n)$的。
证明了节点数是$O(n)$的之后，我们还需要证明边数是$O(n)$的。
考虑一颗$SAM$的生成树（跟$Parent$树）无关。
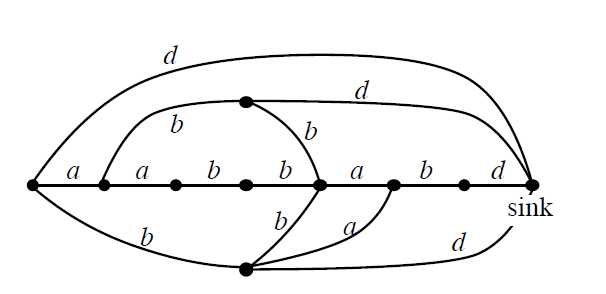令状态数为$M$，一共$M-1$条边，并且一个后缀对应自己遇到的第一条非树边（一条边可能对应多个后缀），刚好能够对应，而后缀个数为$O(n)$的，于是边数也是$O(n)$的。
我们不可能保存每一个状态的$Right$集合，但是一个状态的$Right$集合能由它子树中的叶子$Right$集合的并集。
对于一个状态$s$，设$r_i\in right(s)$，$right(trans(s,x))=\{r_i+1|S[r_i]==x\}$。
【线性构造SAM分析】
设当前字符串为$T$，$T$的长度为$L$，将新加入一个字符$x$。
设所有表示$T$的后缀（也就是$Right$中包含L）的状态$v_1, v_2, v_3, ...$
必然存在一个状态$p=ST(T)$满足$right(p)=\{L\}$，因为$v_1, v_2, v_3, ...$都包含$L$，所以他们在$Parent$树上全是$p$的祖先。
假设我们添加一个字符$x$后，用$np$表示$ST(Tx)$，那么$right(np)={L+1}$。
设$v1=p, v_2, .., v_k=root$，即按深度递减排序，所以$v_1, v_2, v_3, ...$的$Right$大小递增，且如果$v_i$的某位置出发有$x$的边，那么$v_{i+1}$也有。如果$v_j$出发没有$x$的边，那么直接可以把它向$np$连一条$x$的边，因为它的$Right$集合中有$L$。
设$v_p$是$v_1, v_2, v_3, ...$中第一个某个位置出发有$x$边的状态，令$trans(v_p, x)=q$，那么$right(q)=\{r_i+1|s[r_i]=x\}$，注意此时$x$还没有加进字符串里。
难点来了，$x$加进字符串里之后，我们不能直接在$right(q)$中加入$L+1$。
举例子:
$T=aaabaaaabaa$, $x=b$ 也就是$Tx=aaabaaaabaab$。
将$T$中$v_p$代表的某个字符串用括号标记：$a(aa)baa(aa)b(aa)$
将$T$中$q$代表的某个字符串用括号标记：$(aaab)a(aaab)aa$
此时加入$b$，会发现$L+1$加入后可以代表$aab$，但是不能代表$aaab$，所以并不能直接在$right(q)$中加入$L+1$。
当然如果$len(v_p)+1==len(q)$的话也是可以直接加入$L+1$的。
解决上面问题的方法就是新建一个节点$nq$，显然$right(nq)=right(q)\cup (right(np)=\{L+1\})$，就能够解决这个问题了。
于是$trans(v_p~v_k, x)=nq,trans(v_1~v_{p-1}, x)=q$，然后再连接一下$Parent$树就完成构造过程了。
【线性构造SAM步骤】
①新建节点$np$代表$ST(Tx)$。
②自$Parent$树的叶子节点$L$向上找到第一个有出边$x$的$Right$集合包含L的状态$v_p$，途中没有出边$x$的节点都向$np$连边，即$trans(v_1~v_{p-1}, x)=np$。
③若没有$v_p$，则$Parent$树上$np$连向$root$
④新建节点$nq$，复制一次$q$，并进行以下更新
$fa(nq)=fa(q)$//此时的$q$是加入$x$以前的$q$
$fa(q)=fa(np)=nq$
⑤$v_p~v_k$向$nq$连边，即$trans(v_p~v_k)=nq$。
然后就没有了。
注意点数是$2n$的！
代码如下：
#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<algorithm> #define ll long long using namespace std; const int maxn=2000010, inf=1e9; struct poi{int len, fa, trans[26];}st[maxn]; int n, tott, now, root; char s[maxn]; inline void extend(int ch) { int np=++tott, p=now;; st[np].len=st[now].len+1; now=np; while(p && !st[p].trans[ch]) st[p].trans[ch]=np, p=st[p].fa; if(!p) st[np].fa=root; else { int q=st[p].trans[ch]; if(st[p].len+1==st[q].len) st[np].fa=q; else { int nq=++tott; st[nq]=st[q]; st[nq].len=st[p].len+1; st[q].fa=st[np].fa=nq; while(p && st[p].trans[ch]==q) st[p].trans[ch]=nq, p=st[p].fa; } } } int main() { scanf("%s", s+1); n=strlen(s+1); now=tott=root=1; for(int i=1;i<=n;i++) extend(s[i]-‘a‘); }
【例题时间】