Description
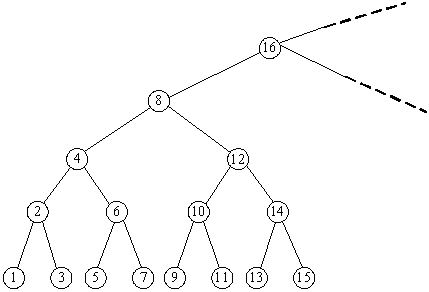
Consider an infinite full binary search tree (see the figure below), the numbers in the nodes are 1, 2, 3, .... In a subtree whose root node is X, we can get the minimum number in this subtree by repeating going down the left node until the last level, and
we can also find the maximum number by going down the right node. Now you are given some queries as "What are the minimum and maximum numbers in the subtree whose root node is X?" Please try to find answers for there queries.
Input
In the input, the first line contains an integer N, which represents the number of queries. In the next N lines, each contains a number representing a subtree with root number X (1 <= X <= 231 - 1).
Output
There are N lines in total, the i-th of which contains the answer for the i-th query.
Sample Input
2
8
10
Sample Output
1 15
9 11
本题就考了树状数组的最最基本操作,对于会树状数组的人来说是太水了。
附个精简得不得了的代码,时间效率是O(1)
#include <stdio.h>
int main()
{
int T, x;
scanf("%d", &T);
while (T--)
{
scanf("%d", &x);
printf("%d %d\n", x-(x&(-x))+1, x+(x&(-x))-1);
}
return 0;
}
POJ 2309 BST 树状数组基本操作,布布扣,bubuko.com
POJ 2309 BST 树状数组基本操作
原文:http://blog.csdn.net/kenden23/article/details/36876881
