1. 首先看到网上说,有个以下公式,只要能把cos(2pai/n)用有理数用四则运算和平方根表示出来,正N变形就可以用尺规证明,反之则不能,那么我估计是因为用尺规只能算出四则运算和平方根。
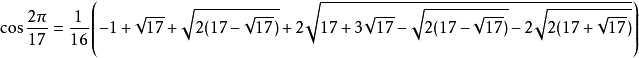
2. 看下具体的计算过程
正十七边形的证明方法
正十七边形的尺规作图存在之证明:
设正17边形中心角为a,则17a=360度,即16a=360度-a
故sin16a=-sina,而
sin16a=2sin8acos8a=2*2sin4acos4acos8a=2*4 sinacosacos2acos4acos8a
因sina不等于0,两边除之有:
16cosacos2acos4acos8a=-1
又由2cosacos2a=cosa+cos3a等,有
2(cosa+cos2a+…+cos8a)=-1 (这一步没证明)
注意到 cos15a=cos2a,cos12a=cos5a,令
x=cosa+cos2a+cos4a+cos8a
y=cos3a+cos5a+cos6a+cos7a
有:
x+y=-1/2
又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)
=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)
经计算知xy=-1
又有
x=(-1+根号17)/4,y=(-1-根号17)/4
其次再设:x1=cosa+cos4a,x2=cos2a+cos8a
y1=cos3a+cos5a,y2=cos6a+cos7a
故有x1+x2=(-1+根号17)/4
y1+y2=(-1-根号17)/4
最后,由cosa+cos4a=x1,cosacos4a=(y1)/2
可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出
尺规作法
步骤一:
给一圆O,作两垂直的直径OA、OB,
作C点使OC=1/4OB,
作D点使∠OCD=1/4∠OCA,
作AO延长线上E点使得∠DCE=45度。
步骤二:
作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,
再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
步骤三:
过G4作OA垂直线交圆O于P4,
过G6作OA垂直线交圆O于P6,
则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点。
