n<=5000个数轴上的点,有属性x,a,b,c,d,从i跳到j的代价如下: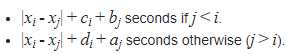
问从s跳到t的最小代价。
方法?:先构造s->t链,然后依次插入其他点,每次选个最佳的位置。过了这题,正确性不明。
方法:从边的向左向右入手。从左到右计算时,有些点想射出一条边却还射不出,有些点想被一条边插上却没边插他,好吧那这些待插(边方向向左)待射(边方向向右)的边决定了状态。同时可以愉快地发现平时出边(右)和入边(左)是一样多的,遇到s时入边(向左)少一条,遇到t时出边(向右)少一条,这可开个变量记。
那$f(i,j)$--前i个点,j条边向右的最小代价,转移比较复杂:
如果i+1是点s,f(i,j)可以转移到f(i+1,j+1)和f(i,j);
如果i+1是点t,f(i,j)可以转移到f(i+1,j-1)和f(i,j);
否则,f(i,j)可以转移到f(i+1,j),f(i+1,j-1),f(i+1,j+1)。
当然这跟当前剩下的射出边(向右)和待入边(向左)是否足够(>0)有关。因此要判断转移的合法。
小细节:未到终态,且不在s和t之间时,向右边0的状态不合法!!

1 #include<string.h> 2 #include<stdlib.h> 3 #include<stdio.h> 4 #include<math.h> 5 //#include<assert.h> 6 #include<algorithm> 7 //#include<iostream> 8 using namespace std; 9 10 int n,s,t; 11 #define maxn 5011 12 #define LL long long 13 int a[maxn],b[maxn],c[maxn],d[maxn],xx[maxn]; 14 LL f[maxn][maxn]; 15 int main() 16 { 17 scanf("%d%d%d",&n,&s,&t); 18 for (int i=1;i<=n;i++) scanf("%d",&xx[i]); 19 for (int i=1;i<=n;i++) scanf("%d",&a[i]); 20 for (int i=1;i<=n;i++) scanf("%d",&b[i]); 21 for (int i=1;i<=n;i++) scanf("%d",&c[i]); 22 for (int i=1;i<=n;i++) scanf("%d",&d[i]); 23 24 for (int i=0;i<=n;i++) 25 for (int j=0;j<=n;j++) 26 f[i][j]=1e18; 27 f[0][0]=0; 28 int havest=0; 29 for (int i=0;i<n;i++) 30 { 31 if (i==s) havest--; 32 if (i==t) havest++; 33 (i && (havest==0) && (f[i][0]=1e18)); 34 for (int j=0;j<=n;j++) if (f[i][j]!=1e18) 35 { 36 if (i+1==s) 37 { 38 if (j+havest) f[i+1][j]=min(f[i+1][j],f[i][j]+xx[i+1]+c[i+1]); 39 f[i+1][j+1]=min(f[i+1][j+1],f[i][j]-xx[i+1]+d[i+1]); 40 } 41 else if (i+1==t) 42 { 43 if (j) f[i+1][j-1]=min(f[i+1][j-1],f[i][j]+xx[i+1]+a[i+1]); 44 f[i+1][j]=min(f[i+1][j],f[i][j]-xx[i+1]+b[i+1]); 45 } 46 else 47 { 48 if (j) f[i+1][j]=min(f[i+1][j],f[i][j]+a[i+1]+d[i+1]); 49 if (j+havest) f[i+1][j]=min(f[i+1][j],f[i][j]+b[i+1]+c[i+1]); 50 if (j && j+havest) f[i+1][j-1]=min(f[i+1][j-1],f[i][j]+2*xx[i+1]+a[i+1]+c[i+1]); 51 f[i+1][j+1]=min(f[i+1][j+1],f[i][j]-2*xx[i+1]+b[i+1]+d[i+1]); 52 } 53 } 54 } 55 printf("%lld\n",f[n][0]); 56 return 0; 57 }

