刚刚开始刷题的时候就栽了个大跟头,稍微记一下。。。。。。
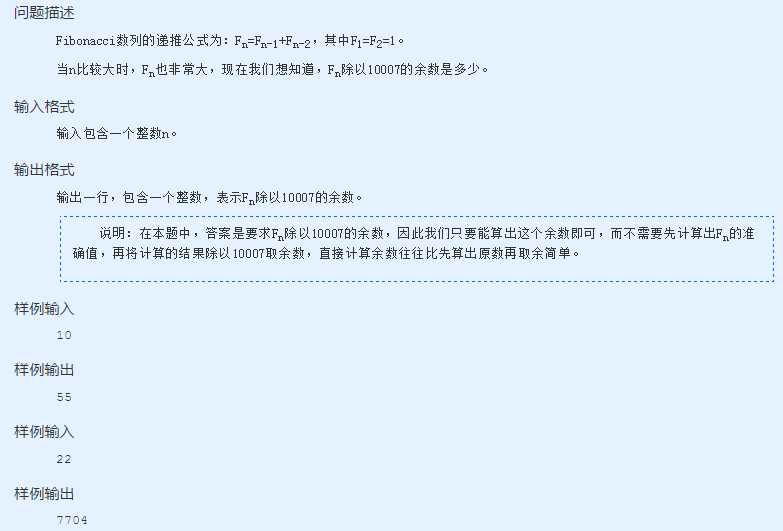

一开始不是很理解:“我们只要能算出这个余数即可,而不需要先计算出Fn的准确值,再将计算的结果除以10007取余数,直接计算余数往往比先算出原数再取余简单”这句话。
写完代码测试后才发现 当Fn 很大的时候,会超出int的表示范围,
后来才想明白为什么要这么做
1 import java.util.Scanner; 2 3 public class Main { 4 public static void main(String[] args) 5 { 6 int n = new Scanner(System.in).nextInt(); 7 int[] Fibonacci = new int[n]; 8 for(int i= 0; i<Fibonacci.length;i++) 9 { 10 if(i==0 || i==1) 11 Fibonacci[i]=1; 12 if(i>1) 13 Fibonacci[i] = (Fibonacci[i-2] + Fibonacci[i-1]) % 10007; 14 } 15 16 System.out.println(Fibonacci[n-1]); 17 } 18 }
假设
Fibonacci[i-2] = x
Fibonacci[i-1] = y
Fibonacci[ i ] =( x + y ) % 10007
如果不求余数,它的值可以如下表示:
Fibonacci[i-2] = ( num1 * 10007 ) + x;
Fibonacci[i-1] = ( num2 * 10007 ) + y;
Fibonacci[ i ] = Fibonacci[i-2] + Fibonacci[i-1] = ( (num1+num2)*10007 + x + y )