今日集训第一日,遇到了判断线段相交问题。跟面积问题一样,这个同样可以用叉积来解决。
数学原理证明:
首先引出计算几何学中一个最基本的问题:如何判断向量在
的顺时针方向还是逆时针方向?
把p0定为原点,p1的坐标是(x1,y1),p2的坐标是(x2,y2)。向量的叉积(cross product)实际上就是矩阵的行列式:
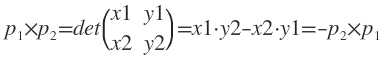
代码实现:
1 int direction(Point p0, Point p1, Point p2) { 2 int px02 = p2.x - p0.x; 3 int py02 = p2.y - p0.y; 4 int px01 = p1.x - p0.x; 5 int py01 = p1.x - p0.y; 6 return px01 * py02 - py01 * px02; 7 }
当叉积为正时,说明在
的顺时针方向上;叉积为0说明两向量共线(同向或反向)。
当同时满足:
(1)和
在
的两侧(即一个顺时针方向上,一个在逆时针方向上)
(2)和
在
的两侧
时可肯定和
相交。

图1
图1是线段相交的一般情形。
图2只满足第(1)条,不满足第(2)条所以不能证明和
相交。
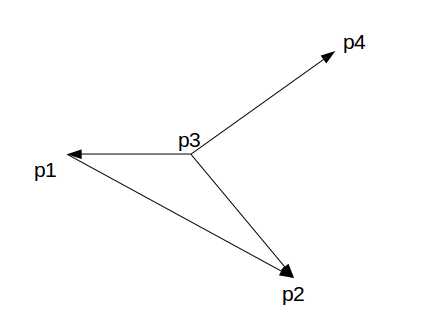
图2
图3和图4是一种特殊情况,它不满足第(2)条,因为和
重合,即
和
的叉积为0。
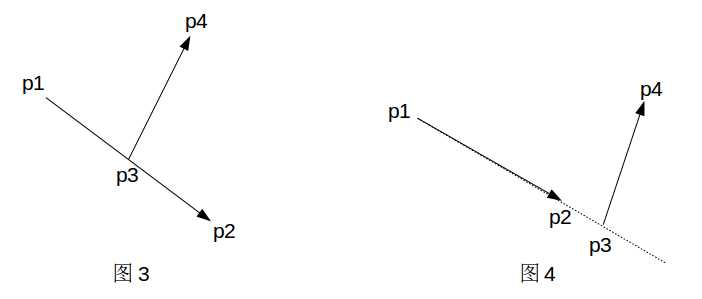
可见当叉积为0时要分情况讨论,当p3在线段p1p2上时两线段相交;当p3在线段p1p2的延长线上时两线段不相交。
证明部分转自:博客园(华夏35度)http://www.cnblogs.com/zhangchaoyang 作者:Orisun
在我自己学习与做题过程中,发现主要要注意的是关注当一线段的端点落在另一线段上的情况要特殊讨论。
此时叉积为0。只要满足如下条件:
1 bool on_segment(Point p0, Point p1, Point p2) { 2 int minx, maxx, miny, maxy; 3 minx = min(p0.x, p1.x); 4 maxx = max(p0.x, p1.x); 5 miny = min(p0.y, p1.y); 6 maxy = max(p0.y, p1.y); 7 if (p2.x >= minx && p2.x <= maxx && p2.y >= miny && p2.y <= maxy) 8 return true; 9 else 10 return false; 11 }
就可以判断此端点在线段上。
由此,我们可以得出判断部分代码。
bool segments_intersect(Point p1, Point p2, Point p3, Point p4) { int d1 = direction(p3, p4, p1); int d2 = direction(p3, p4, p2); int d3 = direction(p1, p2, p3); int d4 = direction(p1, p2, p4); if (d1 * d2 < 0 && d3 * d4 < 0) return true; else if (d1 == 0 && on_segment(p3, p4, p1)) return true; else if (d2 == 0 && on_segment(p3, p4, p2)) return true; else if (d3 == 0 && on_segment(p1, p2, p3)) return true; else if (d4 == 0 && on_segment(p1, p2, p4)) return true; else return false; }
Vane_Tse On the Road. 2014-07-09 00:08:27
原文:http://www.cnblogs.com/slimjerk/p/3832738.html