一、鸽巢原理的证明
1.定义:
若有n个鸽巢和kn+1只鸽子,所有的鸽子都进入鸽巢,那么至少有一个巢中有k+1只鸽子(n,k≥0)。
2.证明(反证法):
若每个鸽巢中的鸽子数都不大于k,则总鸽子数<=kn,与已知相悖。得证。
3.拉姆齐(Ramsey)定理的证明:6个人中,要么存在三个人彼此互相认识,要么存在三个人彼此都不认识;
证明:设六个人为六个点,认识或不认识用两种不同颜色的线段代表,因为两人只有一种关系,所以任意一点一定会引出连向其他5点的五个线段,根据鸽巢定理,有2种关系,有2*2+1=5条关系线,即k=2,
那么必定有一种关系拥有2k+1=3条关系线,得证。
4.中国剩余定理(孙子定理)的证明:
求证:设N,M除了1以外没有公约数(即N,M互质),两个数字a,b满足0≤a<N, 0≤b<M,则恰好存在且仅存在一个数字c满足0≤C<N*M且c除以n的余数为a,除以m的余数为b。
证明(反证法):设存在两个不等的数0≤C1,C2<n*m,使C1,C2关于N,M均同余,即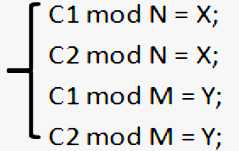
那么我们不妨设C1<C2,那么设k=C2-C1,那么显然,C2-C1为N,M的整数倍,即k为N,M的公倍数,则有kmin=LCM[N,M];
因为N,M互质,由LCM求值公式知,那么k=LCM[N,M]=NM;那么C2=C1+K=C1+NM>=N*M,与假设相悖。得证。
关于LCM可参考以前的随笔:http://www.cnblogs.com/COLIN-LIGHTNING/p/8371664.html;
5.一些数学定理的证明:
①求证:有理数中的无限位小数在小数点后某一位必开始循环。
证明:由有理数定义我们可设该有理数为N/M(N,M∈Z且M!=0),那么根据竖式除法的原则,求值过程中不断更新的是分子N的值,由于不同分子都是由上次的分子对分母取模所得知,去M个不同的分子,那么根据鸽巢原理,他们中至少有两个数关于M同余,那么下一位结果也就循环了。得证。
②求证:从1到2n中,选n + 1个数,至少有一对数,其中一个数是另一个数的倍数;
证明:将选中的n+1个数中所有的2都除掉,即除以2^k,由于1-2n中只有n个奇数,一定有一对数的奇数形式是相等的。这两个数分别是2^mequal,2^nequal,因此一定一个数是另一个数的倍数。得证。
③求证:从1-2n中,选n+1个数,至少有一对数是互素的;
证明:我们可以将[1,2n]划分为n个区间[1,2],[3,4],......,[2n-1,2n],那么n+1个数中至少有两个数来自同一区间;由相邻两数互质知n+1个数中,至少有一对数是互素的。
具体关于互质的证明可以参考以前关于最大公约数的性质的随笔:http://www.cnblogs.com/COLIN-LIGHTNING/p/8371664.html;
④求证:对于任意正整数 n ,都能找到一个 n 的倍数,它全由数字 0 和 1 构成,且前半部分全部为1,后半部分全部为0;
证明:我们取n个数1,11,111,1111,......,i个1,由鸽巢原理知,这n个数中对n取模至少有两个数相同,设较大的数为M,较小的数为m,则易证n|M-m;因为M为长度大于m的1串,那么相减后M-m前半部分一定全部为1,后半部分全部为0;
二、相关题目
1.[POJ2356]Find a multiple
Description
Description
The input contains N natural (i.e. positive integer) numbers ( N <= 10000 ). Each of that numbers is not greater than 15000. This numbers are not necessarily different (so it may happen that two or more of them will be equal). Your task is to choose a few of given numbers ( 1 <= few <= N ) so that the sum of chosen numbers is multiple for N (i.e. N * k = (sum of chosen numbers) for some natural number k).
Input:The first line of the input contains the single number N. Each of next N lines contains one number from the given set.
Output:
In case your program decides that the target set of numbers can not be found it should print to the output the single number 0. Otherwise it should print the number of the chosen numbers in the first line followed by the chosen numbers themselves (on a separate line each) in arbitrary order.
if there are more than one set of numbers with required properties you should print to the output only one (preferably your favorite) of them.
Solution
1.题目大意即为求n个数中区间和被n整除的第一个区间[l,r];
2.由鸽巢原理知,n个不同的数会造成n个不同的前缀和,那么至少有两个前缀和关于n是同余的,我们只需找出第一个出现两次的模后前缀和即可;
3.打一个时间标记,记录模值的第一次出现地址,当第二次出现同一模后前缀和时,使l=第一次出现地址,r=第二次出现地址,区间[l,r]即为所求;
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){
int i,j,l=0,r,n,t[10001]={},a[10001]={},sum[10001]={};
scanf("%d",&n);
memset(t,-1,sizeof(t));
t[0]=0;
for(i=1;i<=n;++i){
scanf("%d",&a[i]);
sum[i]=(sum[i-1]+a[i])%n;
if(t[sum[i]]!=-1){
l=t[sum[i]];
r=i;
break;
}
else t[sum[i]]=i;//zzh大佬的计数方法;
}
printf("%d\n",r-l);
for(i=l+1;i<=r;++i)printf("%d\n",a[i]);
return 0;
}