定义:
回归是统计学的核心,它其实是一个广义的概念,通常指那些用一个或多个预测变量来预测响应变量.既:从一堆数据中获取最优模型参数
1.线性回归
1.1简单线性回归
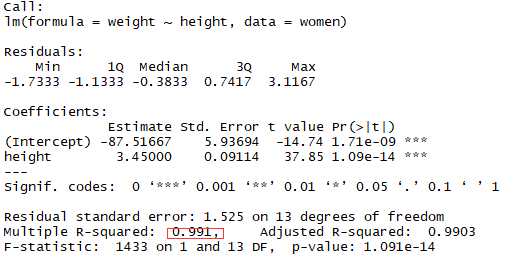
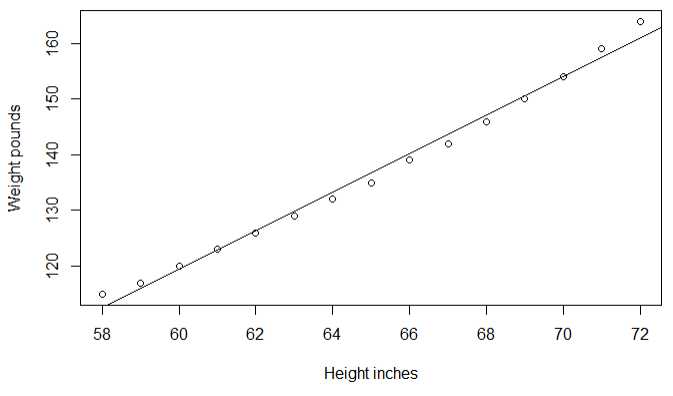
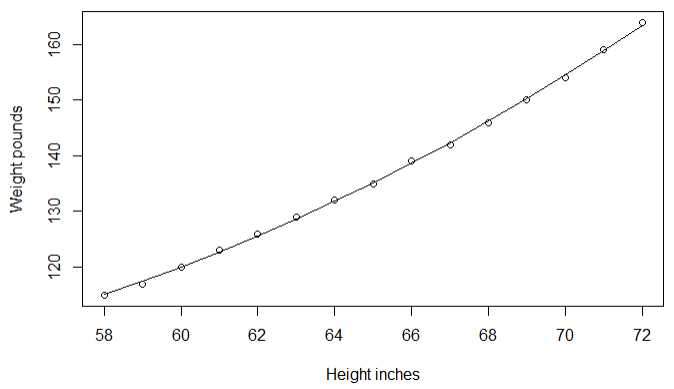
案例:女性预测身高和体重的关系
结论:身高和体重成正比关系
1 fit <- lm(weight ~ height,data = women) 2 summary(fit) 3 plot(women$height,women$weight,xlab = ‘Height inches‘,ylab = ‘Weight pounds‘) 4 abline(fit)
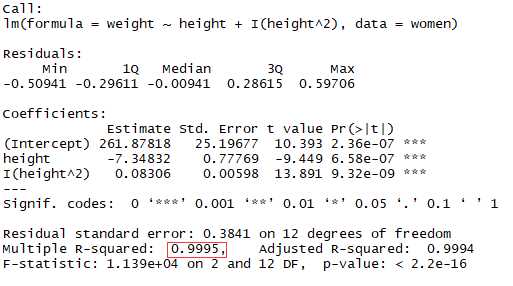
1.2添加多项式来提升预测精度
结论:模型的方差解释率提升到99.9%,表示二次项提高了模型的拟合度
1 fit2 <- lm(weight ~ height + I(height^2),data = women) 2 summary(fit2) 3 plot(women$height,women$weight,xlab = ‘Height inches‘,ylab = ‘Weight pounds‘) 4 lines(women$height,fitted(fit2))
1.3多元线性回归
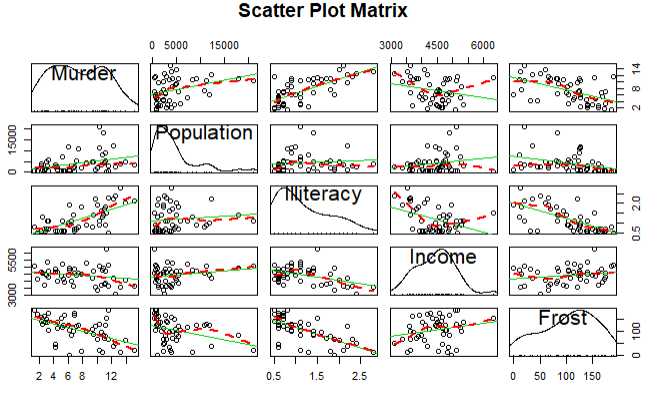
案例探究:探究美国州的犯罪率和其他因素的关系,包括人口,文盲率,平均收入,天气
结论:谋杀率和人口,文盲率呈正相关,和天气,收入呈负相关
1 states <- as.data.frame(state.x77[,c("Murder", "Population", 2 "Illiteracy", "Income", "Frost")]) 3 cor(states) 4 library(car) 5 scatterplotMatrix(states,spread = F,smoother.args = list(lty=2),main=‘Scatter Plot Matrix‘)

结论:文盲率的回归系数是4.14,说明在控制其他变量不变的情况下,文盲率提升1%,谋杀率就会提高4.14%
# 多元线性回归
1 fit3 <- lm(Murder~Population+Illiteracy+Income+Frost,data = states) 2 summary(fit3)

1.4回归诊断
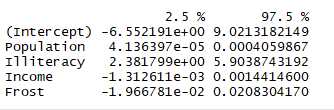
结论:文盲率改变1%,谋杀率在95%的置信区间[2.38,5.9]之间变化,因为frost的置信区间包含0,所以可以认为温度的改变与谋杀率无关
1 confint(fit3)
结论:除了Nevada一个点,其余的点都很好的符合了模型
1 par(mfrow=c(2,2)) 2 plot(fit3)
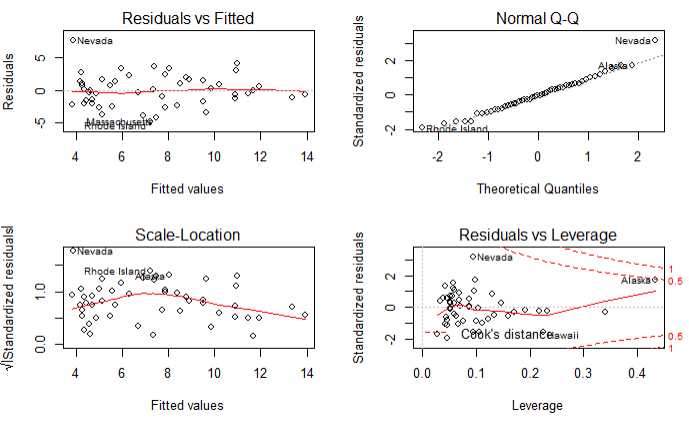
学生化残差分布图展示了除了Nevada一个离群点,其他点都很好的符合了模型
1 residplot <- function(fit,nbreaks=10){ 2 z <- rstudent(fit) 3 hist(z,breaks = nbreaks,freq = F,xlab = ‘Studentized Residual‘,main = ‘Distribution of Errors‘) 4 rug(jitter(z),col = ‘brown‘) 5 curve(dnorm(x,mean=mean(z),sd=sd(z)),add=T,col=‘blue‘,lwd=2) 6 lines(density(z)$x,density(z)$y,col=‘red‘,lwd=2,lty=2) 7 legend(‘topright‘,legend = c(‘Normal Curve‘,‘KernelDensity Curve‘),lty = 1:2,col = c(‘blue‘,‘red‘),cex = .7) 8 } 9 10 residplot(fit3)
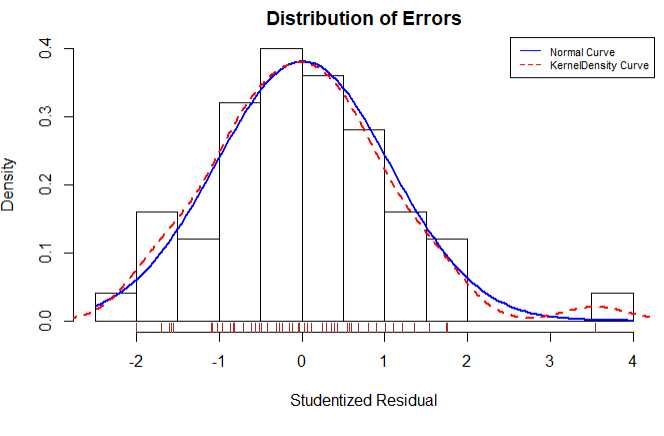
1.5 异常观测值
1.5.1 离群点:指的是模型预测观测效果
此处可以看到Nevada是数据集中的离群点
1 library(car) 2 outlierTest(fit3)

1.5.2 高杠杆值点:与其他观测变量有关的离群点
可以通过以下的帽子图进行观测,,一般来说若帽子值的均值大于帽子均值的2倍或者3倍,就是高杠杆点
1 hat.plot <- function(fit){ 2 p <- length(coefficients(fit3)) 3 n <- length(fitted(fit3)) 4 plot(hatvalues(fit3),main = ‘Index Plot of Hat Values‘) 5 abline(h=c(2,3)*p/n,col=‘red‘,lty=2) 6 identify(1:n,hatvalues(fit3),names(hatvalues(fit3))) 7 } 8 hat.plot(fit3)
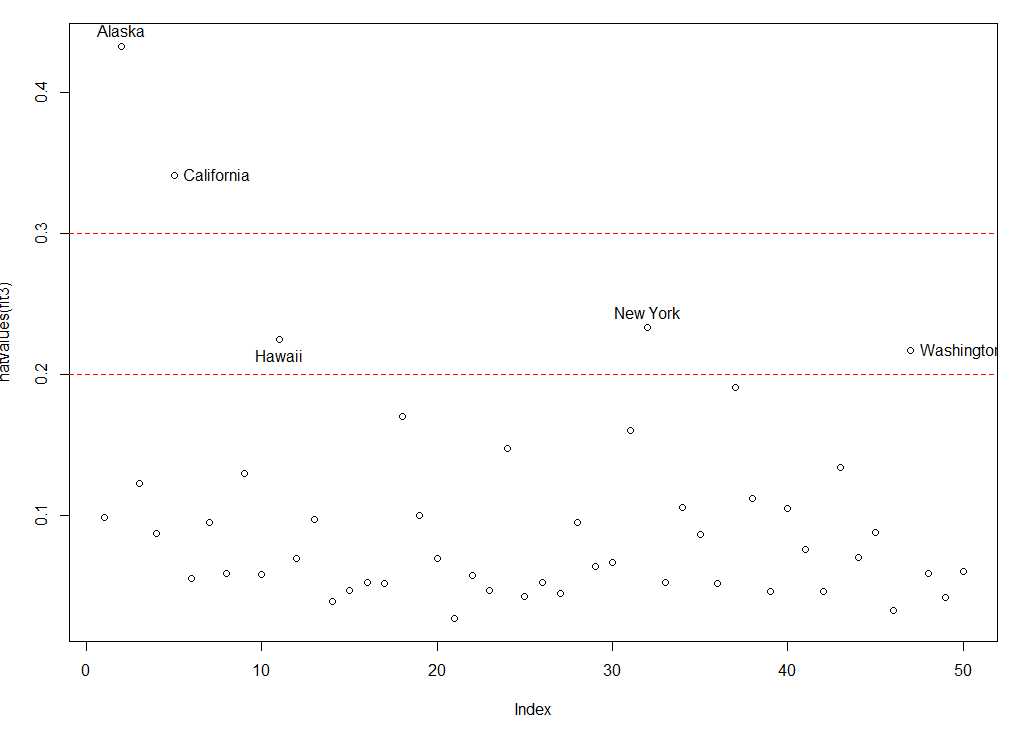
1.5.3强影响点:对模型参数影响有比例失调的点
使用cook‘s D值大于4/(n-k-1)表示是强影响点
1 cutoff <- 4/(nrow(states)-length(fit3$coefficients)-2) 2 plot(fit3,which=4,cook.levels=cutoff) 3 abline(h=cutoff,lty=2,col=‘red‘)
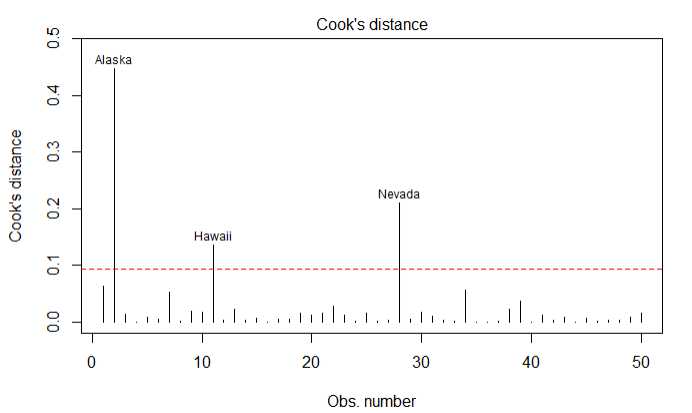
1.5.4还可以通过气泡图来展示哪些是离群点,强影响点和高杠杆值点
1 influencePlot(fit3,id.method=‘identify‘,main=‘Infulence Plot‘,sub=‘Circle size is proportional to cook distance‘)
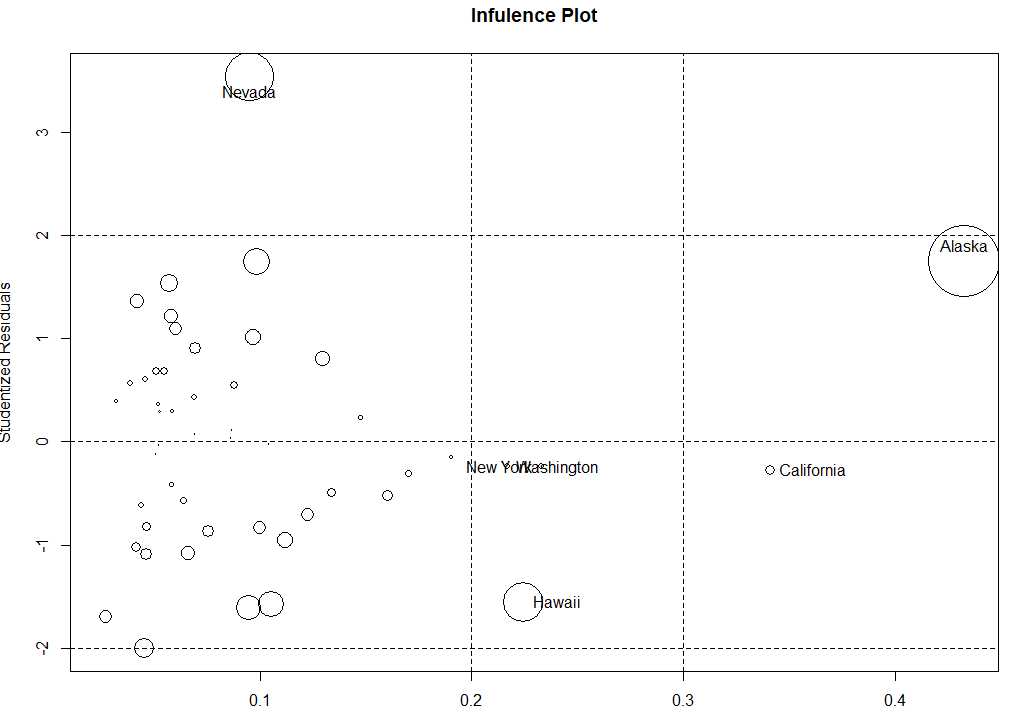
1.6选择最佳的模型
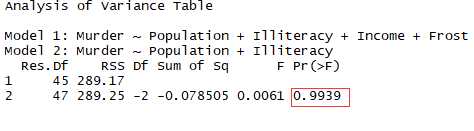
1.6.1使用anova比较
结论:由于检验不显著,不需要吧Income和Forst加入到变量中
1 fit5 <- lm(Murder ~ Population+Illiteracy,data = states) 2 anova(fit3,fit5)
1.6.2使用AIC比较
结论:同上
1 fit5 <- lm(Murder ~ Population+Illiteracy,data = states) 2 AIC(fit3,fit5)

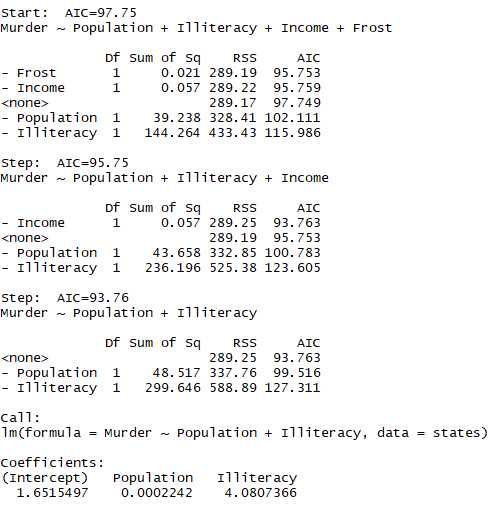
1.6.3变量选择
结论:开始时模型包含4个变量,在每一步中,AIC列提供了一个删除变量后的AIC值第一次删除AIC从97.75下降到95.75,第二次从93.76,再删除变量会增加AIC所以回归停止
1 library(MASS) 2 stepAIC(fit3,direction = ‘backward‘)
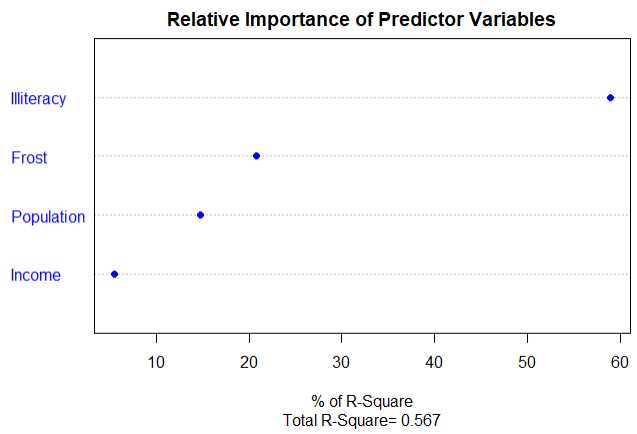
1.6.4使用自定义韩式计算相对权重
结论:可以看到每个预测变量对模型方差的解释程度和影响权重
1 relweights <- function(fit,...){ 2 R <- cor(fit$model) 3 nvar <- ncol(R) 4 rxx <- R[2:nvar,2:nvar] 5 rxy <- R[2:nvar,1] 6 svd <- eigen(rxx) 7 evec <- svd$vectors 8 ev <- svd$values 9 delta <- diag(sqrt(ev)) 10 lambda <- evec %*% delta %*% t(evec) 11 lambdasq <- lambda ^ 2 12 beta <- solve(lambda) %*% rxy 13 rsquare <- colSums(beta ^ 2) 14 rawwgt <- lambdasq %*% beta ^ 2 15 import <- (rawwgt / rsquare) * 100 16 import <- as.data.frame(import) 17 row.names(import) <- names(fit$model[2:nvar]) 18 names(import) <- ‘Weights‘ 19 import <- import[order(import),1,drop=F] 20 dotchart(import$Weights,labels = row.names(import),xlab = ‘% of R-Square‘,pch=19, 21 main = ‘Relative Importance of Predictor Variables‘, 22 sub=paste(‘Total R-Square=‘,round(rsquare,digits = 3)),...)
23 return(import)
# 调用
24 relweights(fit3,col=‘blue‘)