1、动态规划是通过组合字问题的解而解决整个问题的。
2、它与分治法的区别:
分治法是将问题分解为一些独立的子问题,递归的求解各个子问题,然后合并子问题的解而得到源问题的解。
而动态规划适合用于子问题不是独立的情况,也就是各个子问题包含公共的子子问题。在这种情况下,若采用分治的的思想则会做许多不必要的工作。动态规划会对每个子子问题之求解一次,将其结果保存在一张表中,从而避免每次遇到各个子问题时重新计算答案。
3、设计步骤:(应用于最优化问题)
1):描述最优解的结构。
2):递归定义最优解的值。
3):按自底向上的方式计算最优解的值
4):由计算出的结果构造一个最优解
eg:装配线调度:汽车公司在生产汽车的时候,有两条转配线,如图。汽车地盘在进入每一条装配线后,在每条先上安装完各个部件后离开。每一条装配线上有n个装配站,编号问j = 1,2,,,n。将装配线i(i为1或者2)的第j个装配站表示为S(i,j)。第j站的功能相同,比如S(1,3)与S(2,3).然而每个站上的装配时间是不相同的。我们把装配站S(i,j)上的时间记为a(i,j)。一个汽车底盘在进入和离开装配线i的时候都需要花费时间,地盘进入装配线i的时间为ei;装配完离开装配线的时间为xi,从一个装配线移走的时间为t(i,j);
一旦一个地盘进入一条装配线后,它只会经过该条装配线。在相同的装配线中,从一个装配站到下一个装配站所花的时间可以忽略。偶尔会来一个特别急得订单,客户要求尽可能快的制造这些汽车。会转移到别的装配线上,这时会有进入和离开的时间。
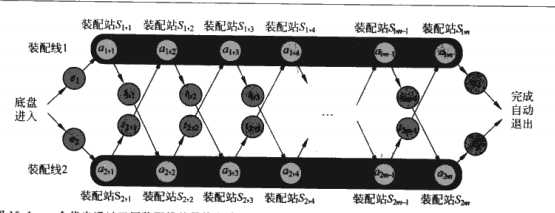
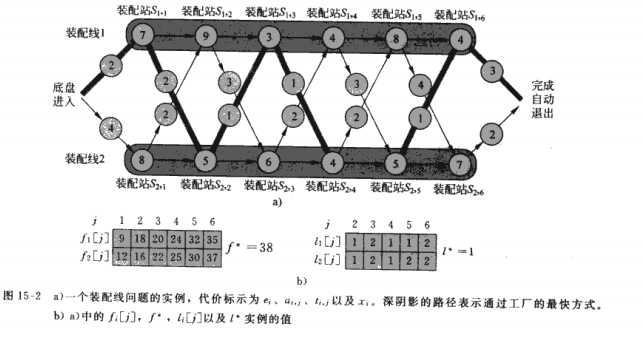
步骤一:通过工厂最快路线的结构
动态规划的第一个步骤是描述最优解的结构的特征
首先,假设通过装备站S(1,j)的最快路线通过了装配站S(1,j-1)。关键的一点是地盘必定利用了最快的路线从开始点到装配站S(2,j-1)。
对于装配线调度问题,一个问题的(找出通过装配站S(i,j)的最快路线)最优解包含的子问题(找出通过S(i,j-1)或S(2,j-1)的最快路线)的一个最优解。我们称这个性质为最优子结构,这是是否可以应用动态规划方法的标志之一。
我们可以利用最优子结构的最优解来构造源问题的一个最优解。对于装配线调度问题的推理如下:
观察一条通过装匹配站S(1,j)的最快路线,会发现必定是经过装配线1或2上的装配站j-1.因此,通过装配站S(1,j)的最快路线只能是一下二者之一;
a、通过装配站S(1,j-1)的最快路线,然后直接通过装配站S(1,j)。
b、通过装配站S(2,j-1)的最快路线,从装配线2移动到装配线1,然后通过装配站S(1,j)。
利用对称的推理思想,通过装配站S(2,j)的最快路线也和上边一样。
为了解决这个问题,及寻找通过任一条装配线上的装配站j的最快路线,我们解决他的子问题,即寻找通过两条线配线上的装配站j-1的最快路线。
所以,对于装配线调度问题,通过建立子问题的最优解,就可以建立源问题某个势力的一个最优解
步骤二:一个递归的解
在动态规划的方法中,第二个步骤是利用子问题的最优解来递归定义一个最优解的值。对于装配线的调度问题,我们选择在两条装配线上通过装配线j的最快路线的问题来作为子问题,j = 1,2,。。。。,n。另f[j]表示一个地盘从起点到装配站最快可能时间。
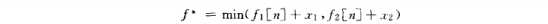
要对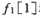 和
和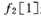 进行推理是很简单的,因为不管是哪一条我们都可以直达,所以:
进行推理是很简单的,因为不管是哪一条我们都可以直达,所以:
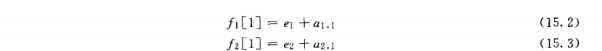
接下来我们就要计算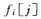 ,加入我们要计算
,加入我们要计算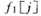 ,则有;
,则有;
![]()
对应的的装配线2:
![]()
合并上述公式可以得到:
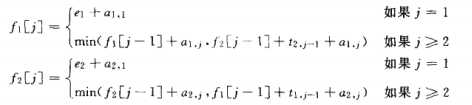
我们继续定义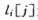 ,
,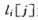 内放置装配线的编号(1或2),其中的装配站j-1被通过装配站的S(1,j)的最快路线所使用。
内放置装配线的编号(1或2),其中的装配站j-1被通过装配站的S(1,j)的最快路线所使用。
步骤三:计算最快时间
此时,我们可以更具上边的公式写出一个递归算法来计算通过工厂的最快路线还是比较简单的。但是这种递归算发会出现一个问题,更具最后的递归式,我们会得到他的执行时间是有关于n的指数形式。
如果在递归的方式中以不同的顺序来计算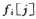 的值,可以做的更好,通过递增的方式来计算
的值,可以做的更好,通过递增的方式来计算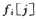 ,可以在O(n)时间内计算出通过工厂的最快路线。
,可以在O(n)时间内计算出通过工厂的最快路线。

