一般在推荐系统中，数据往往是使用 用户-物品 矩阵来表示的。用户对其接触过的物品进行评分，评分表示了用户对于物品的喜爱程度，分数越高，表示用户越喜欢这个物品。而这个矩阵往往是稀疏的，空白项是用户还未接触到的物品，推荐系统的任务则是选择其中的部分物品推荐给用户。
（markdown写表格太麻烦了，直接上传图片吧）
对于这个 用户-物品 矩阵，可以利用非空项的数据来预测空白项的数据，即预测用户对于其未接触到的物品的评分，并根据预测情况，将评分高的物品推荐给用户。预测评分的方式有很多，本篇主要讲述如何使用矩阵分解来进行这个预测。
1.奇异值分解SVD
想详细理解SVD，推荐一篇博客 奇异值分解(SVD)原理与在降维中的应用。
此时可以将这个 用户-物品 对应的m×n矩阵 M 进行 SVD 分解，并通过选择部分较大的一些奇异值来同时进行降维，也就是说矩阵M此时分解为：
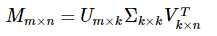
（不知道如何在 markdown 中输入公式，先用图片代替）
其中，m 是用户的维度，n 是物品的维度，k 是矩阵 M 的较大的 k 个奇异值，k 往往远小于 m 和 n，这也是 SVD 可以用来降维的原因。
如果我们要预测第 i 个用户对第 j 个物品的评分 mij ,则只需要计算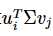 
即可。通过这种方法，我们可以将评分表里面所有没有评分的位置得到一个预测评分。通过找到最高的若干个评分对应的物品推荐给用户。
——待续——