作用:1、求方程的根,2、最优化。
首先,选择一个接近函数 零点的
零点的 ,计算相应的
,计算相应的 和切线斜率
和切线斜率 (这里
(这里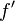 表示函数
表示函数 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点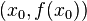 并且斜率为
并且斜率为 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:

x就是新求得的点,
x=x0-f(x0)/f’(x0)
我们不妨将新求得的点x记为x1,则
x1=x0-f(x0)/f‘(x0)
很明显可以用迭代公式,则
xn+1=xn-f(xn)/f‘(xn)
先看一张静态图:
最终xn+1就是一个非常接近最有点的解。具体可以看维基百科的动态图 。
原文:http://www.cnblogs.com/menghuizuotian/p/3835303.html