原题:ZOJ 3774 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3774
----------------------------------------------------------------------------------------------------------------------
这题比较复杂,看这篇比较详细:http://blog.csdn.net/acdreamers/article/details/23039571
结论就是计算:
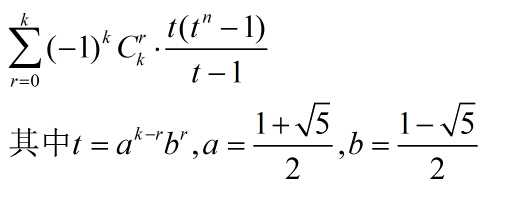
充分利用了快速幂及求逆元。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <cstdlib> #include <algorithm> #define Mod 1000000009 #define ll long long using namespace std; #define N 100007 ll fac[N],A[N],B[N]; void init() { int i; fac[0] = 1; for(i=1;i<N;i++) fac[i] = fac[i-1]*i%Mod; A[0] = B[0] = 1; for(i=1;i<N;i++) { A[i] = A[i-1]*691504013 % Mod; B[i] = B[i-1]*308495997 % Mod; } } ll fastm(ll n,ll k,ll MOD) { ll res = 1LL; n %= MOD; while(k) { if(k&1LL) res = (res*n)%MOD; k >>= 1; n = n*n%MOD; } return res; } ll Inv(ll n,ll MOD) { return fastm(n,MOD-2,MOD); } int main() { int cs; ll n,k; init(); ll ans,r; scanf("%d",&cs); while(cs--) { scanf("%lld%lld",&n,&k); ans = 0; for(r=0;r<=k;r++) { ll t = A[k-r]*B[r] % Mod; ll x = fac[k]; // k! ll y = fac[k-r]*fac[r] % Mod; // (k-r)!*(r)! ll c = x*Inv(y,Mod) % Mod; // c = C(k,r) = x/y = x*Inv(y) ll tmp = t*(fastm(t,n,Mod)-1)%Mod*Inv(t-1,Mod)%Mod; //t(t^n-1)/(t-1) = t(t^n-1)*Inv(t-1) if(t == 1) tmp = n%Mod; tmp = tmp*c%Mod; if(r&1LL) // (-1)^r ans -= tmp; else ans += tmp; ans %= Mod; } //ans = ans*(1/sqrt(5))^k ll m = Inv(383008016,Mod)%Mod; ans = ans*fastm(m,k,Mod)%Mod; ans = (ans%Mod+Mod)%Mod; printf("%lld\n",ans); } return 0; }
2014 Super Training #7 F Power of Fibonacci --数学+逆元+快速幂,布布扣,bubuko.com
2014 Super Training #7 F Power of Fibonacci --数学+逆元+快速幂
原文:http://www.cnblogs.com/whatbeg/p/3836551.html