All rights reserved. Please don‘t share this article without notifying me. Email address: westonhunter@zju.edu.cn
From eq. 10 in part 1 we can find the Classical Gram Schmidt Algorithm, which is numerically unstable or sensitive to perturbation:
Q=zeros((m,n))
R=zeros((n,n))
for k= 1 to n
tmpk=cAk
for i= 1 to k-1
R[i][k]=cAk^T*cQi
tmpk=tmpk-R[i][k]*cQi
R[k][k]=||tmpk||
cQk=tmpk/R[k][k]
Q calculated by Classical Gram Schmidt algorithm is not very orthogonal due to rounding errors. An example is provided by X. Jiao[1]
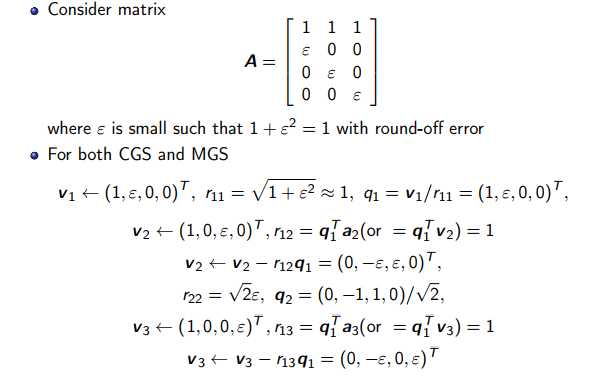
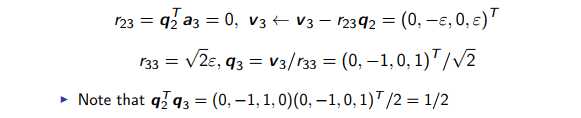
The error introduced in q1 also cause errors in q2 and q3. We will discuss how to avoid this in the next part.
[1] http://www.ams.sunysb.edu/~jiao/teaching/ams526_fall11/lectures/lecture06.pdf
