差点儿全部编程语言中都提供了"生成一个随机数"的方法,也就是调用这种方法会生成一个数,我们事先也不知道它生成什么数。比方在.Net中编写以下的代码:
Random rand = newRandom();
Console.WriteLine(rand.Next());
|
执行后结果例如以下:

Next()方法用来返回一个随机数。相同的代码你执行和我的结果非常可能不一样,并且我多次执行的结果也非常可能不一样,这就是随机数。
一、陷阱
看似非常easy的东西,使用的时候有陷阱。我编写以下的代码想生成100个随机数:
for(int
i=0;i<100;i++) { Random rand =
new Random();
Console.WriteLine(rand.Next());
} |
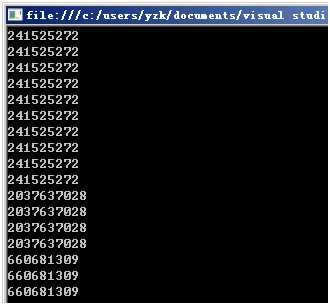
太奇怪了,居然生成的"随机数"有好多连续一样的,这算什么"随机数"呀。有人指点"把new Random()"放到for循环外面就能够了:
Random rand = newRandom();
for(int
i=0;i<100;i++) {
Console.WriteLine(rand.Next());
} |
执行结果:
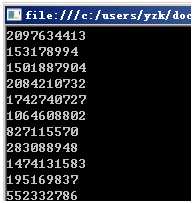
确实能够了!
二、这是为什么呢?
这要从计算机中"随机数"产生的原理说起了。我们知道,计算机是非常严格的,在确定的输入条件下,产生的结果是唯一确定的,不会每次运行的结果不一样。那么怎么样用软件实现产生看似不确定的随机数呢?
生成随机数的算法有非常多种,最简单也是最经常使用的就是 "线性同余法": 第n+1个数=(第n个数*29+37) % 1000,当中%是"求余数"运算符。非常多像我一样的人见了公式都头疼,我用代码解释一下吧,MyRand是一个自己定义的生成随机数的类:
class
MyRand {
private
int seed; public
MyRand(int
seed) {
this.seed = seed;
}
public
int Next()
{
int
next = (seed * 29 + 37) % 1000; seed = next;
return
next; }
} |
例如以下调用:
MyRand rand = newMyRand(51);
for
(int i = 0; i < 10; i++)
{
Console.WriteLine(rand.Next());
}
|
运行结果例如以下:
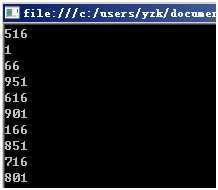
生成的数据是不是看起来"随机"了。简单解释一下这个代码:我们创建MyRand的一个对象,然后构造函数传递一个数51,这个数被赋值给seed,每次调用Next方法的时候依据(seed * 29 + 37) % 1000计算得到一个随机数,把这个随机数赋值给seed,然后把生成的随机数返回。这样下次再调用Next()的时候seed就不再是51,而是上次生成的随机数了,这样就看起来好像每一次生成的内容都非常"随机"了。注意"%1000"取余预算的目的是保证生成的随机数不超过1000。
当然不管是你执行还是我每次执行,输出结果都是一样的随机数,由于依据给定的初始数据51,我们就能够依次判断下来以下生成的全部"随机数"是什么都能够算出来了。这个初始的数据51就被称为"随机数种子",这一系列的516、1、66、951、616……数字被称为"随机数序列"。我们把51改成52,就会有这种结果:
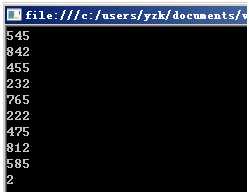
三、楼主好人,跪求种子
那么怎么能够使得每次执行程序的时候都生成不同的"随机数序列"呢?由于我们每次执行程序时候的时间非常可能不一样,因此我们能够用当前时间做"随机数种子"
MyRand rand = newMyRand(Environment.TickCount);
for
(int i = 0; i < 10; i++)
{
Console.WriteLine(rand.Next());
}
|
Environment.TickCount为"系统启动后经过的毫秒数"。这样每次程序执行的时候Environment.TickCount都不大可能一样(靠手动谁能一毫秒内启动两次程序呢),所以每次生成的随机数就不一样了。
当然假设我们把new MyRand(Environment.TickCount)放到for循环中:
for
(int i = 0; i < 100; i++)
{
MyRand rand = newMyRand(Environment.TickCount);
Console.WriteLine(rand.Next());
}
|
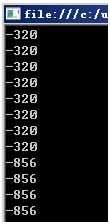
执行结果又变成"非常多是连续"的了,原理非常easy:因为for循环体执行非常快,所以每次循环的时候Environment.TickCount非常可能还和上次一样(两行简单的代码执行用不了一毫秒那么长事件),因为这次的"随机数种子"和上次的"随机数种子"一样,这样Next()生成的第一个"随机数"就一样了。从"-320"变成"-856"是因为执行到"-856"的时候时间过了一毫秒。
四、各语言的实现
我们看到.Net的Random类有一个int类型參数的构造函数:
public Random(int Seed)
就是和我们写的MyRand一样接受一个"随机数种子"。而我们之前调用的无參构造函数就是给Random(int Seed)传递Environment.TickCount类进行构造的,代码例如以下:
public Random() : this(Environment.TickCount)
{
}
这下我们最终明确最開始的疑惑了。
相同道理,在C/C++中生成10个随机数不应该例如以下调用:
int
i; for(i=0;i<10;i++)
{ srand( (unsigned)time( NULL ) );
printf("%d\n",rand());
} |
而应该:
|
|
srand( (unsigned)time( NULL ) );
//把当前时间设置为"随机数种子" int
i; for(i=0;i<10;i++)
{ printf("%d\n",rand());
} |
五、"奇葩"的Java
Java学习者可能会提出问题了,在Java低版本号中,例如以下使用会像.Net、C/C++中一样产生同样的随机数:
for(int
i=0;i<100;i++)
{ Random rand =
new Random();
System.out.println(rand.nextInt());
} |
由于低版本号Java中Rand类的无參构造函数的实现相同是用当前时间做种子:
public Random() { this(System.currentTimeMillis()); }
可是在高版本号的Java中,比方Java1.8中,上面的"错误"代码运行却是没问题的:
为什么呢?我们来看一下这个Random无參构造函数的实现代码:
public
Random() { this(seedUniquifier() ^ System.nanoTime());
} <br>private
static long
seedUniquifier() { for
(;;) { long
current = seedUniquifier.get();
long
next = current * 181783497276652981L; if
(seedUniquifier.compareAndSet(current, next)) return
next; }
}
privatestaticfinal AtomicLong seedUniquifier =
new AtomicLong(8682522807148012L);
|
这里不再是使用当前时间来做"随机数种子",而是使用System.nanoTime()这个纳秒级的时间量而且和採用原子量AtomicLong依据上次调用构造函数算出来的一个数做异或运算。关于这段代码的解释具体參考这篇文章《解密随机数生成器(2)——从java源代码看线性同余算法》
最核心的地方就在于使用static变量AtomicLong来记录每次调用Random构造函数时使用的种子,下次再调用Random构造函数的时候避免和上次一样。
六、高并发系统中的问题
前面我们分析了,对于使用系统时间做"随机数种子"的随机数生成器,假设要产生多个随机数,那么一定要共享一个"随机数种子"才会避免生成的随机数短时间之内生成反复的随机数。可是在一些高并发的系统中一个不注意还会产生问题,比方一个站点在server端通过以下的方法生成验证码:
Random rand = new Random();
Int code = rand.Next();
当站点并发量非常大的时候,可能一个毫秒内会有非常多个人请求验证码,这就会造成这几个人请求到的验证码是反复的,会给系统带来潜在的漏洞。
再比方我今天看到的一篇文章《当随机不够随机:一个在线扑克游戏的教训》里面就提到了"因为随机数产生器的种子是基于server时钟的,黑客们仅仅要将他们的程序与server时钟同步就行将可能出现的乱序降低到仅仅有 200,000 种。到那个时候一旦黑客知道 5 张牌,他就能够实时的对 200,000 种可能的乱序进行高速搜索,找到游戏中的那种。所以一旦黑客知道手中的两张牌和 3 张公用牌,就能够猜出转牌和河牌时会来什么牌,以及其它玩家的牌。"
这样的情况有例如以下几种解决方法:
七、真随机数发生器
依据我们之前的分析,我们知道这些所谓的随机数不是真的"随机",仅仅是看起来随机,因此被称为"伪随机算法"。在一些对随机要求高的场合会使用一些物理硬件採集物理噪声、宇宙射线、量子衰变等现实生活中的真正随机的物理參数来产生真正的随机数。
当然也有聪明的人想到了不借助添加"随机数发生器"硬件的方法生成随机数。我们操作计算机时候鼠标的移动、敲击键盘的行为都是不可预測的,外界命令计算机什么时候要运行什么进程、处理什么文件、载入什么数据等也是不可预測的,因此导致的CPU运算速度、硬盘读写行为、内存占用情况的变化也是不可预測的。因此假设採集这些信息来作为随机数种子,那么生成的随机数就是不可预測的了。
在Linux/Unix下能够使用"/dev/random"这个真随机数发生器,它的数据主来来自于硬件中断信息,只是产生随机数的速度比較慢。
Windows下能够调用系统的CryptGenRandom()函数,它主要根据当前进程Id、当前线程Id、系统启动后的TickCount、当前时间、QueryPerformanceCounter返回的高性能计数器值、username、计算机名、CPU计数器的值等等来计算。和"/dev/random"一样CryptGenRandom()的生成速度也比較慢,并且消耗比較大的系统资源。
当然.Net下也能够使用RNGCryptoServiceProvider 类(System.Security.Cryptography命名空间下)来生成真随机数,依据StackOverflow上一篇帖子介绍RNGCryptoServiceProvider 并非对CryptGenRandom()函数的封装,可是和CryptGenRandom()原理类似。
八、总结
有人可能会问:既然有"/dev/random" 、CryptGenRandom()这种"真随机数发生器",为什么还要提供、使用伪随机数这种"假货"?由于前面提到了"/dev/random" 、CryptGenRandom()生成速度慢并且比較消耗性能。在对随机数的不可预測性要求低的场合,使用伪随机数算法就可以,由于性能比較高。对于随机数的不可预測性要求高的场合就要使用真随机数发生器,真随机数发生器硬件设备须要考虑成本问题,而"/dev/random"、CryptGenRandom()则性能较差。
万事万物都没有完美的,没有绝对的好,也没有绝对的坏,这才是多元世界美好的地方。
随机数是骗人的,.Net、Java、C为我作证,布布扣,bubuko.com
原文:http://www.cnblogs.com/mengfanrong/p/3837553.html