1.实验内容
- 函数声明和函数定义:
- 形参和实参: 主调函数把实参的值传送给被调函数的形参从而实现主调函数向被调函数的数据传送。
- 形参:形式参数,表示主调函数与被调函数之间的联系。标识了在形参出现的位置应该有一个什么类型的数据。 特性:在调用时才分配内存空间,用完即释放。
- 实参:实参可以是常量、变量、表达式、函数等, 无论实参是何种类型的量,在进行函数调用时,它们都必须具有确定的值, 以便把这些值传送给形参
- 返回值的作用:1.返回函数的运算结果。 2.return; 用于结束当前的函数执行。
- 函数的参数传递:
-
- 值传递:单向值传递 函数调用时,给形参分配内存空间,并由实参对形参进行初始化。一旦形参获得值便与实参脱离,此后形参不再影响实参。
- 引用传递:作用:子函数中形参做的更改对实参有效。声明一个引用时,必须对他进行初始化,使它指向一个存在的对象,并且不能再指向其他对象。引用作为形参时,初始化在调用该函数时发生,这样引用类型的形参就成了实参的别名,对形参的修改可以直接作用于实参。
2.题目及代码:
-
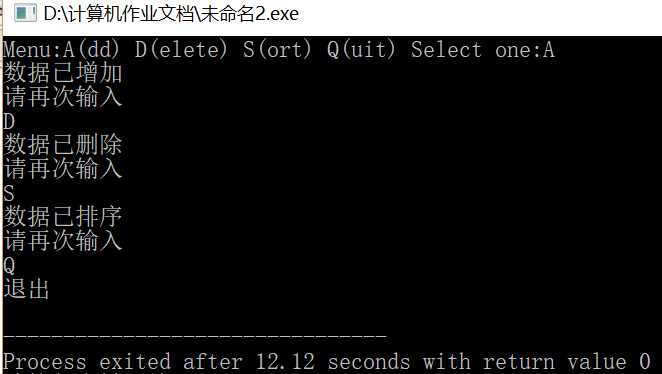
- 实现一个简单的菜单程序输入。运行时显示“Menu:A(dd) D(elete) S(ort) Q(uit) Select one:”,输入A D S Q分别表示数据的增加,删除,排序,退出。(分别运用if...else,switch )第一个用if else 实现
 View Code
View Code1 #include<iostream> 2 using namespace std; 3 //使用if...else 4 int main(){ 5 char n; 6 cout<<"Menu:A(dd) D(elete) S(ort) Q(uit) Select one:"; 7 while(cin>>n){ 8 9 if(n==‘A‘) 10 cout<<"数据已增加"<<endl; 11 else if(n==‘D‘) 12 cout<<"数据已删除"<<endl; 13 else if(n==‘S‘) 14 cout<<"数据已排序"<<endl; 15 else{ 16 cout<<"退出"<<endl; 17 break;} 18 cout<<endl; 19 cout<<"请再次输入"<<endl; 20 } 21 return 0; 22 23 }
用switch实现
 View Code
View Code1 #include<iostream> 2 using namespace std; 3 int main(){ 4 char n; 5 cout<<"Menu:A(dd) D(elete) S(ort) Q(uit) Select one:"; 6 while(cin>>n){ 7 switch(n){ 8 case ‘A‘:{ 9 cout<<"数据已增加"<<endl; 10 break;} 11 case ‘D‘:{ 12 cout<<"数据已删除"<<endl; 13 break; 14 } 15 case ‘S‘:{ 16 cout<<"数据已排序"<<endl; 17 break; 18 } 19 case ‘Q‘:{ 20 cout<<"退出"<<endl; 21 break; 22 } 23 } 24 if(n==‘Q‘) 25 break; 26 cout<<"请再次输入"<<endl; 27 28 } 29 return 0; 30 }
- 实现一个简单的菜单程序输入。运行时显示“Menu:A(dd) D(elete) S(ort) Q(uit) Select one:”,输入A D S Q分别表示数据的增加,删除,排序,退出。(分别运用if...else,switch )第一个用if else 实现
-
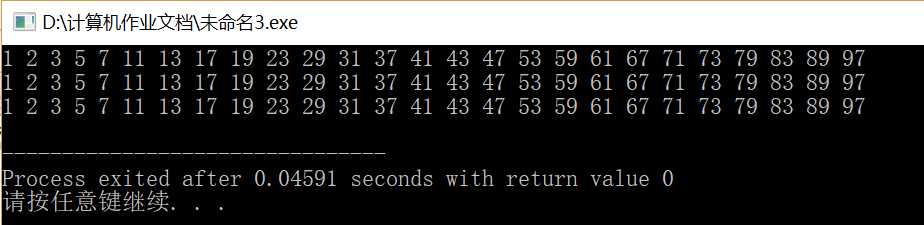
- 用穷举法找出1—100之间的质数并显示出来。
思路:将判断质数单独写成一个函数,如果一个数从2开始到他本身都没有能整除他的数即为质数。利用三个子函数(分别采用while,do...while,for)输出打印质数。

1 #include<iostream> 2 using namespace std; 3 //判断质数:1到sqrt(n)都没有能整除它的数 4 int zspan(int n){ 5 int i; 6 for( i=2;i<n;i++){ 7 if(n%i==0)break; 8 } 9 if(i>=n) return 1; 10 else return 0; 11 } 12 //输出质数 三种不同的循环语句实现 13 int coutzhishu1(int n){ 14 while(n<=100){ 15 if(zspan(n)) 16 cout<<n<<" "; 17 n++; 18 }cout<<endl; 19 return 0; 20 } 21 int coutzhishu2(int n){ 22 do{ 23 if(zspan(n)) 24 cout<<n<<" "; 25 n++; 26 }while(n<100); 27 cout<<endl; 28 return 0; 29 } 30 int coutzhishu3(int n){ 31 for(int i=n;i<=100;i++){ 32 if(zspan(i)) 33 cout<<i<<" "; 34 } 35 cout<<endl; 36 return 0; 37 } 38 39 40 int main(){ 41 int n=1; 42 coutzhishu1(n); 43 coutzhishu2(n); 44 coutzhishu3(n); 45 return 0; 46 }
-
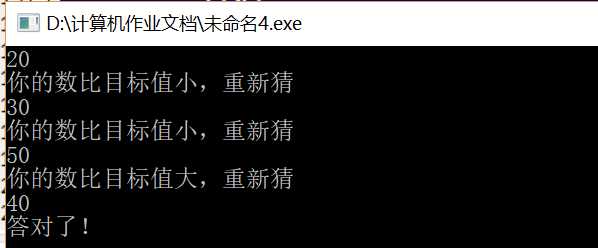
- 题目:在程序中定义一个整型变量,赋予1-100的值。要求用户猜这个数,比较两个数的大小,把结果提供给用户,直到猜对为止。
 View Code
View Code1 #include<iostream> 2 using namespace std; 3 int main() 4 { 5 int i=40; 6 int n; 7 while( cin>>n){ 8 if(n!=40){ 9 if(n<40) 10 {cout<<"你的数比目标值小,重新猜"<<endl; 11 continue; 12 } 13 else{ 14 cout<<"你的数比目标值大,重新猜"<<endl; 15 continue; 16 } 17 } 18 else{ cout<<"答对了!"<<endl; 19 break;} 20 } 21 }
-
题目:口袋中有红黄蓝白黑5种颜色的球若干个,每次从口袋中取出3个颜色不同的球。问有几种取法。
 View Code
View Code1 #include<iostream> 2 using namespace std; 3 enum color{ red,yellow,blue,white,black 4 }; 5 int main(){ 6 int i,j,k,n=0; 7 for(i=red;i<=black;i++){ 8 for(j=red;j<=black;j++){ 9 if(i!=j){ 10 for(k=red;k<=black;k++){ 11 if(i!=k&&j!=k){ 12 n=n+1; 13 cout<<i<<j<<k<<" "; 14 } 15 } 16 } 17 } 18 } 19 cout<<"一共取法:"<<n<<endl; 20 return 0; 21 22 }

- 题目:在程序中定义一个整型变量,赋予1-100的值。要求用户猜这个数,比较两个数的大小,把结果提供给用户,直到猜对为止。
3.第三章收获:
-
- 递归算法:实质是将原有问题分解成新的问题,解决新问题又用到原有问题的解。最终的子问题,是一个已知的解,合并起来能形成原问题的解。步骤:
- 递推:将原问题不断的分解为新的问题。一直到最小已知的解答项。
- 回归:从已知条件出发,逐一求值回归、。

- 递归的运行机制:
- 计算当前函数的实参值
- 分配空间,并将首地址压栈
- 转到函数体,执行语句,递归调用
- 到出口值,从栈顶取出相应的数据,回收空间,转到上一层的调用位置继续执行本次调用未完成的语句。直到取出最后一个值,返回结果。
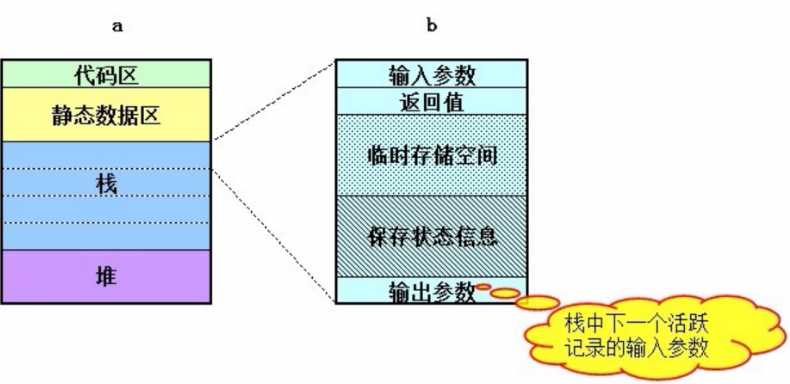
- 递归的效率:递归调用具体要保存的内容包括:局部变量、形参、调用函数地址、返回值。那么,如果递归调用N次,就要分配N*局部变量、N*形参、N*调用函数地址、N*返回值。这势必是影响效率。递归就是利用系统的堆栈保存函数当中的局部变量来解决问题的,并且这些变量一直不被释放,直到遇到简单情境时才一一出栈释放,所以总的开销就很大。如何改进递归效率是一个需要思考的问题。c++中提供一个inline函数,可以避免参数压栈。能不能用在递归里面?
- 内联函数:不是在调用时发生转移,而是在编译时将函数体嵌入在每一个调用处。这样在被调用处进行代码展开,就省去了参数压栈、栈帧开辟与回收,结果返回等,从而提高程序运行速度。但是在书中P82页上注明,对自身直接调用的递归函数不能使用。原因是,内联函数只是程序员给编译器的一个建议,而递归函数被调用之前也不知道自己要被调用多少次的函数,展开过于庞大,使得代码臃肿。
- 递归函数转化成非递归:迭代:就是利用已知的值推算出下一步的值,可以避免调用栈。大多数的递归都可以转化成迭代函数,使用迭代效率更高,但是没有递归表达更清晰。
- 举例:斐波那契数列:
 View Code
View Code1 #include <iostream> 2 using namespace std; 3 4 //迭代实现斐波那契数列 5 long fab_iteration(int index) 6 { 7 if(index == 1 || index == 2) 8 { 9 return 1; 10 } 11 else 12 { 13 long f1 = 1L; 14 long f2 = 1L; 15 long f3 = 0; 16 for(int i = 0; i < index-2; i++) 17 { 18 f3 = f1 + f2; //利用变量的原值推算出变量的一个新值 19 f1 = f2; 20 f2 = f3; 21 } 22 return f3; 23 } 24 } 25 26 //递归实现斐波那契数列 27 long fab_recursion(int index) 28 { 29 if(index == 1 || index == 2) 30 { 31 return 1; 32 } 33 else 34 { 35 return fab_recursion(index-1)+fab_recursion(index-2); //递归求值 36 } 37 } 38 39 int main(int argc, char* argv[]) 40 { 41 cout << fab_recursion(10) << endl; 42 cout << fab_iteration(10) << endl; 43 return 0; 44 }
- 举例:斐波那契数列:
- C++的系统函数:很多函数继承C而来,因此继承自C的函数前缀为c,比如cmath.注意少用math.h。(仅仅是能兼容)推荐网址:http://www.cppreference.com 可以查询标准函数原型,头文件。
- 递归算法:实质是将原有问题分解成新的问题,解决新问题又用到原有问题的解。最终的子问题,是一个已知的解,合并起来能形成原问题的解。步骤:
参考资料:
- 《C++语言程序设计》
- https://www.cnblogs.com/bakari/p/5349383.html
- http://blog.csdn.net/K346K346/article/details/52065524


