上一节讲的三叶结,举一反三,由三可到无穷,这一节讲N叶结
再次看下三叶结的公式:
x = sin(t) + 2*sin(2*t)
y = cos(t) - 2*cos(2*t)
将其改为:
x = sin(t) + 2*sin((n-1)*t)
y = cos(t) - 2*cos((n-1)*t)
就变成了N叶结了,如此简单.
N叶结:
vertices = 12000 t = from 0 to (20*PI) n = rand_int2(2, 24) x = sin(t) + 2*sin(n*t - t) y = cos(t) - 2*cos(n*t - t) z = -sin(n*t) r = 5; x = x*r y = y*r z = z*r

另一种写法:
vertices = 12000 t = from 0 to (20*PI) n = rand_int2(2, 24) x = (2 + cos(n*t))*cos((n - 1)*t) y = (2 + cos(n*t))*sin((n - 1)*t) z = sin(n*t) r = 5 x = x*r y = y*r z = z*r

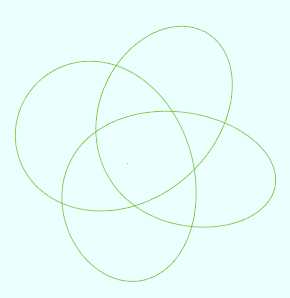
四叶结
#http://www.mathcurve.com/courbes3d/noeuds/noeuddetrefle.shtml vertices = 1000 t = from 0 to (2*PI) r = 10; x = r*(cos(t) + 2*cos(3*t)) z = r*(sin(t) - 2*sin(3*t)) y = r*sin(4*t)
原文:http://www.cnblogs.com/WhyEngine/p/3839982.html