前面讲了N叶结,当N值越大时,你会发现整个图形越像一个圆环.这一节就讲其他几种绕在圆环上的曲线.
vertices = 12000 t = from 0 to (64*PI) p = rand_int2(2, 32) q = rand_int2(2, 32) r = 2 + cos(q/p*t) x = r*sin(t) y = sin(q/p*t) z = r*cos(t) r = 0.5 + 0.5*sin(t) g = 0.5 + 0.5*y b = 0.5 + 0.5*cos(t)
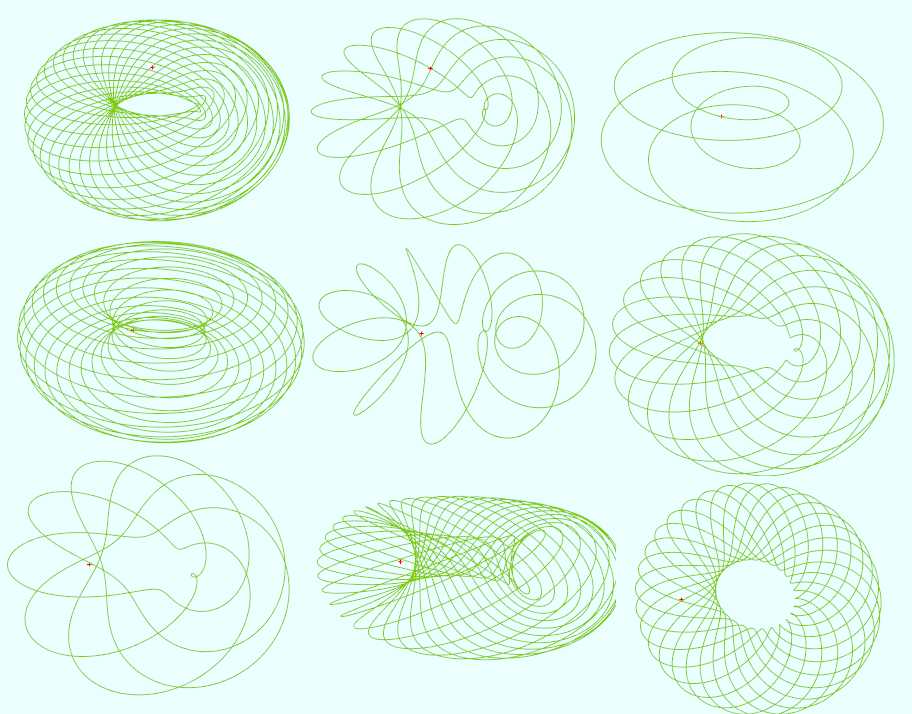
另一个圆环上的曲线
#http://www.mathcurve.com/courbes3d/solenoidtoric/solenoidtoric.shtml vertices = 10000 t = from 0 to (20*PI) n = rand2(0.5, 10) a = rand2(5, 10) b = rand2(1, 5) x = (a + b*cos(n*t))*cos(t) z = (a + b*cos(n*t))*sin(t) y = b*sin(n*t)

knot(huit)
#http://www.mathcurve.com/courbes3d/noeuds/noeudenhuit.shtml vertices = 1000 t = from 0 to (80*PI) x = sin(t) y = sin(t)*cos(t)/2 z = sin(2*t)*sin(t/2) / 4 r = 10; x = x*r y = y*r z = z*r

knot(Paul Bourke)
#http://www.mathcurve.com/courbes3d/noeuds/noeudenhuit.shtml vertices = 1000 t = from 0 to (80*PI) x = 3*cos(t) + 5*cos(3*t) y = 3*sin(t) + 5*sin(3*t) z = sin(5*t/2)*sin(3*t) + sin(4*t) - sin(6*t) r = 4; x = x*r y = y*r z = z*r

knot(Rohit Chaudhary)
#http://www.mathcurve.com/courbes3d/noeuds/noeudenhuit.shtml vertices = 12000 t = from 0 to (2*PI) a = sin(t) b = cos(t) c = sin(2*t) d = cos(2*t) e = sin(3*t) f = cos(3*t) x = 32*b - 51*a - 104*d - 34*c + 104*f - 91*e y = 94*b + 41*a + 113*d - 68*f - 124*e z = 16*b + 73*a - 211*d - 39*c - 99*f - 21*e

knot(37)
vertices = 10000 t = from 0 to (6*PI) p = 3 q = 7 r = 2 + cos(q/p*t) x = r*sin(t) y = sin(q/p*t) z = r*cos(t) r = 0.5 + 0.5*sin(t) g = 0.5 + 0.5*y b = 0.5 + 0.5*cos(t)
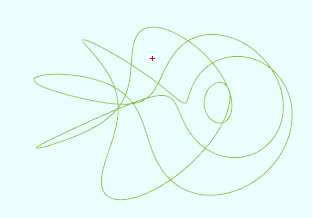
数学图形(2.3)绕在圆环上的曲线,布布扣,bubuko.com
原文:http://www.cnblogs.com/WhyEngine/p/3840009.html