前面发布了很多种二维的曲线图形,其实所有的二维图形再加一个维度值就可以变成三维图形.那么这一节的内容是将一个二维曲线帖到一个球面上,以生成三维曲线.
帖到球上的方式是以如下公式生成第三个维度的数值:
y = sqrt(a*a - x*x - z*z)
这里举个例子是之前发的一种二维曲线:
Cyclic-harmonic_sphere
vertices = 12000 t = from 0 to (40*PI) a = 10 e = 1 n = rand2(0.1, 10); p = a*(1 + e*cos(n*t)) x = p*cos(t) z = p*sin(t) r = array_max(p) y = sqrt(r*r - p*p)

folioide_sphere
#http://www.mathcurve.com/courbes2d/folioide/folioide.shtml vertices = 12000 t = from (-20*PI) to (20*PI) e = rand2(0.1, 10) a = 10 / e i = rand_int2(2, 10) j = rand_int2(1, 10) n = i/j p = a*(e*cos(n*t) + sign(t)*e*sqrt(1 - pow(cos(n*t), 2))) x = p*cos(t) z = p*sin(t) r = array_max(p) y = sqrt(r*r - x*x - z*z)
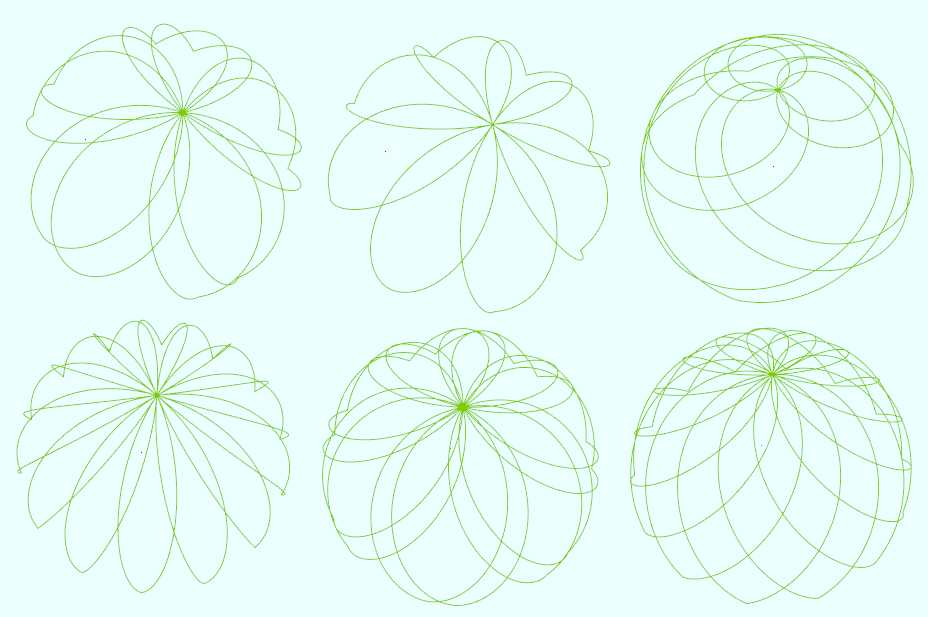
改变一下半径,可以生成一种草帽形的曲线
Cyclic-harmonic_hat
vertices = 12000 t = from 0 to (40*PI) a = 10 e = 1 n = rand2(0.1, 10); p = a*(1 + e*cos(n*t)) x = p*cos(t) z = p*sin(t) y = sqrt(a*a - x*x - z*z)

切图时,我给帽子设置的颜色不太好了,我直到切最后一个图时才意识到.
数学图形(2.11) 帖在球上的曲线图形,布布扣,bubuko.com
原文:http://www.cnblogs.com/WhyEngine/p/3840139.html