Strassen矩阵乘法是通过递归实现的,它将一般情况下二阶矩阵乘法(可扩展到n阶,但Strassen矩阵乘法要求n是2的幂)所需的8次乘法降低为7次,将计算时间从O(nE3)降低为O(nE2.81)。
矩阵C = A*B,可写为
C11 = A11B11 + A12B21
C12 = A11B12 + A12B22
C21 = A21B11 + A22B21
C22 = A21B12 + A22B22
如果A、B、C都是二阶矩阵,则共需要8次乘法和4次加法。如果阶大于2,可以将矩阵分块进行计算。耗费的时间是O(nElg8)即为O(nE3)。
要改进算法计算时间的复杂度,必须减少乘法运算次数。按分治法的思想,Strassen提出一种新的方法,用7次乘法完成2阶矩阵的乘法,算法如下:
S1= B12 - B12
S2= A11 + A12
S3= A21 + A22
S4= B21 - B11
S5= A11 + A22
S6= B11 + B22
S7= A12 - A22
S8= B21 + B22
S9= A11 - A21
S10= B11 + B12
M1 = A11(B12 - B12)
M2 = (A11 + A12)B22
M3 = (A21 + A22)B11
M4 = A22(B21 - B11)
M5 = (A11 + A22)(B11 + B22)
M6 = (A12 - A22)(B21 + B22)
M7 = (A11 - A21)(B11 + B12)
完成了7次乘法,再做如下加法:
C11 = M5 + M4 - M2 + M6
C12 = M1 + M2
C21 = M3 + M4
C22 = M5 + M1 - M3 - M7
全部计算使用了7次乘法和18次加减法,计算时间降低到O(nElg7)约为O(nE2.81)。计算复杂性得到较大改进..
1 #include<stdio.h> 2 #include<math.h> 3 #define N 4 4 5 void main(){ 6 void print(int A[][N],int n); 7 void common(int A[][N],int B[][N],int C[][N],int n); 8 void ADD(int A[][N],int B[][N],int C[][N],int n); 9 void SUB(int A[][N],int B[][N],int C[][N],int n); 10 void STRASSEN(int n,int A[][N],int B[][N],int C[][N]); 11 int A[N][N]; 12 int B[N][N]; 13 int C[N][N]; 14 int i,j,n; 15 n=N; 16 for(i=0;i<n;i++) //构造数组 17 for(j=0;j<n;j++){ 18 A[i][j]=rand()%10; 19 B[i][j]=rand()%10; 20 } 21 printf("数组A:\n"); 22 print(A,n); 23 printf("数组B:\n"); 24 print(B,n); 25 printf("\nC=A*B;数组C:\n"); 26 common(A,B,C,n); 27 print(C,n); 28 printf("\n换方法 Strssen算法:\n"); 29 STRASSEN(n,A,B,C); 30 print(C,n); 31 }// 主函数 32 33 void print(int A[][N],int n){ //输出数组 34 int i ,j; 35 for(i=0;i<n;i++){ 36 for(j=0;j<n;j++) 37 printf("%5d",A[i][j]); 38 printf("\n"); 39 } 40 } 41 42 void common(int A[][N],int B[][N],int C[][N],int n){ //普通求解数组C. T(n)= O(n^3) 43 int i,j,k; 44 for(i=0;i<n;i++) 45 for(j=0;j<n;j++){ 46 C[i][j]=0; 47 for(k=0;k<n;k++) 48 C[i][j]+=A[i][k]*B[k][j]; 49 } 50 } 51 52 void ADD(int A[][N],int B[][N],int C[][N],int n){ 53 int i,j; 54 for(i=0;i<n;i++) 55 for(j=0;j<n;j++) 56 C[i][j]=A[i][j]+B[i][j]; 57 } 58 59 void SUB(int A[][N],int B[][N],int C[][N],int n){ 60 int i,j; 61 for(i=0;i<n;i++) 62 for(j=0;j<n;j++) 63 C[i][j]=A[i][j]-B[i][j]; 64 } 65 66 void STRASSEN(int n,int A[][N],int B[][N],int C[][N]) //STRASSEN函数(递归) 67 { 68 int A11[N][N],A12[N][N],A21[N][N],A22[N][N]; 69 int B11[N][N],B12[N][N],B21[N][N],B22[N][N]; 70 int C11[N][N],C12[N][N],C21[N][N],C22[N][N]; 71 int S1[N][N],S2[N][N],S3[N][N],S4[N][N],S5[N][N],S6[N][N],S7[N][N],S8[N][N],S9[N][N],S10[N][N]; 72 int M1[N][N],M2[N][N],M3[N][N],M4[N][N],M5[N][N],M6[N][N],M7[N][N]; 73 int MM1[N][N],MM2[N][N]; 74 int i,j; 75 76 77 if (n<=2) 78 common(A,B,C,2);//按通常的矩阵乘法计算C=AB的子算法(仅做2阶) 79 else 80 { 81 for(i=0;i<n/2;i++) 82 for(j=0;j<n/2;j++) 83 84 { 85 A11[i][j]=A[i][j]; 86 A12[i][j]=A[i][j+n/2]; 87 A21[i][j]=A[i+n/2][j]; 88 A22[i][j]=A[i+n/2][j+n/2]; 89 B11[i][j]=B[i][j]; 90 B12[i][j]=B[i][j+n/2]; 91 B21[i][j]=B[i+n/2][j]; 92 B22[i][j]=B[i+n/2][j+n/2]; 93 } //将矩阵A和B式分为四块 94 95 SUB(B12,B22,S1,n/2); 96 ADD(A11,A12,S2,n/2); 97 ADD(A21,A22,S3,n/2); 98 SUB(B21,B11,S4,n/2); 99 ADD(A11,A22,S5,n/2); 100 ADD(B11,B22,S6,n/2); 101 SUB(A12,A22,S7,n/2); 102 ADD(B21,B22,S8,n/2); 103 SUB(A11,A21,S9,n/2); 104 ADD(B11,B12,S10,n/2); 105 106 107 STRASSEN(n/2,A11,S1,M1);//M1=A11(B12-B22) 108 STRASSEN(n/2,S2,B22,M2);//M2=(A11+A12)B22 109 STRASSEN(n/2,S3,B11,M3);//M3=(A21+A22)B11 110 STRASSEN(n/2,A22,S4,M4);//M4=A22(B21-B11) 111 STRASSEN(n/2,S5,S6,M5);//M5=(A11+A22)(B11+B22) 112 STRASSEN(n/2,S7,S8,M6);//M6=(A12-A22)(B21+B22) 113 STRASSEN(n/2,S9,S10,M7);//M7=(A11-A21)(B11+B12) 114 //计算M1,M2,M3,M4,M5,M6,M7(递归部分) 115 116 117 118 ADD(M5,M4,MM1,N/2); 119 SUB(M2,M6,MM2,N/2); 120 SUB(MM1,MM2,C11,N/2);//C11=M5+M4-M2+M6 121 122 ADD(M1,M2,C12,N/2);//C12=M1+M2 123 124 ADD(M3,M4,C21,N/2);//C21=M3+M4 125 126 ADD(M5,M1,MM1,N/2); 127 ADD(M3,M7,MM2,N/2); 128 SUB(MM1,MM2,C22,N/2);//C22=M5+M1-M3-M7 129 130 for(i=0;i<n/2;i++) 131 for(j=0;j<n/2;j++) 132 { 133 C[i][j]=C11[i][j]; 134 C[i][j+n/2]=C12[i][j]; 135 C[i+n/2][j]=C21[i][j]; 136 C[i+n/2][j+n/2]=C22[i][j]; 137 } //计算结果送回C[N][N] 138 } 139 }
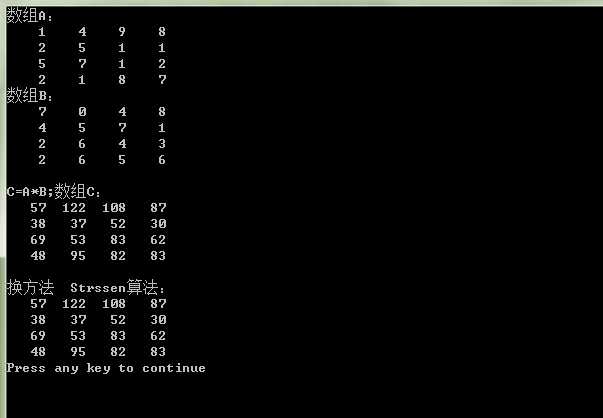
运行结果:
原文:http://www.cnblogs.com/zzsf/p/3840626.html