Surround the Trees

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.



There are no more than 100 trees.

9 
12 7 
24 9 
30 5 
41 9 
80 7 
50 87 
22 9 
45 1 
50 7 
0 

243.06

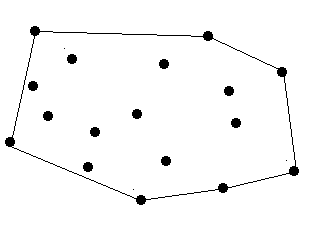
题意是求将所有点围住的那个面积的最小周长。。但是要注意当只有一个点时，也就输出0.00，当只有两个点时。。也就是两点间的距离。。

这是凸包问题的入门题。。。（Orz）   用的是刘汝佳大白上的Andrew算法。。看他的代码实现。。简直丧心病狂。。Orz  。。搞了好久的时间。。智商完全不够用。。

好吧。。因为是今天刚刚接触。。所以一天也就弄了这么一道题。。5555555.。。泪流满面。。。

</pre><pre name="code" class="cpp">

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<sstream>
#include<cmath>

#define f1(i, n) for(int i=0; i<n; i++)
#define f2(i, m) for(int i=1; i<=m; i++)

struct Point
{
    double x, y;
};

void sort(Point *p, int n)  //按照x从小到大排序（如果x相同， 按照y从小到大排序）
{
    Point temp;
    int i, j;
    for(i=0; i<n-1; i++)
        for(j=0; j<n-1-i; j++)
        {
            if(p[j].x>p[j+1].x)
            {
                temp = p[j];
                p[j] = p[j+1];
                p[j+1] = temp;
            }
            if(p[j].x==p[j+1].x && p[j].y>p[j+1].y)
            {
                temp = p[j];
                p[j] = p[j+1];
                p[j+1] = temp;
            }
        }
}


int cross(int x1, int y1, int x2, int y2)   //看P[i]是否是在其内部。。
{
    if(x1*y2-x2*y1<=0)                 //叉积小于0，说明p[i]在当前前进方向的右边，因此需要从凸包中删除c[m-1],c[m-2]
        return 0;
    else
        return 1;
}

int convexhull(Point *p, Point *c, int n)
{
    int i,m=0,k;
    f1(i, n)  //下凸包
    {
        while(m>1 && !cross(c[m-2].x-c[m-1].x,c[m-2].y-c[m-1].y,c[m-1].x-p[i].x,c[m-1].y-p[i].y))
            m--;
        c[m++]=p[i];
    }
    k=m;
    for(i=n-2; i>=0; i--)  //求上凸包
    {
        while(m>k && !cross(c[m-2].x-c[m-1].x,c[m-2].y-c[m-1].y,c[m-1].x-p[i].x,c[m-1].y-p[i].y))
            m--;
        c[m++]=p[i];
    }
    if(n>1)
        m--;
    return m;
}

double dis(Point a, Point b)    //求两个凸包点之间的长度。。
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

int main()
{
    Point a[105], p[105];
    int n, i, m;
    double lenth;
    while(scanf("%d",&n) &&n)
    {
        f1(i, n)
        scanf("%lf %lf",&a[i].x, &a[i].y);

        if(n==1)
        {
            printf("0.00\n");
            continue;
        }
        else if(n==2)
        {
            printf("%.2lf\n", dis(a[0], a[1]));
            continue;
        }
        sort(a, n);
        m=convexhull(a, p, n);
        lenth = 0;
        f2(i, m)
        lenth+=dis(p[i],p[i-1]);
        printf("%.2lf\n",lenth);
    }
    return 0;
}

HDU1392：Surround the Trees（凸包问题）,布布扣,bubuko.com

HDU1392：Surround the Trees（凸包问题）

原文：http://blog.csdn.net/u013487051/article/details/37728857