中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,先左后根再右。巧记:左根右。
现在有一个问题,已知二叉树的前序遍历和中序遍历:
PreOrder: GDAFEMHZ
InOrder: ADEFGHMZ
我们如何还原这颗二叉树,并求出他的后序遍历?
我们基于一个事实:中序遍历一定是 { 左子树中的节点集合 },root,{ 右子树中的节点集合 },前序遍历的作用就是找到每颗子树的root位置。
算法1
输入:前序遍历,中序遍历
1、寻找树的root,前序遍历的第一节点G就是root。
2、观察前序遍历GDAFEMHZ,知道了G是root,剩下的节点必然在root的左或右子树中的节点。
3、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树中的节点,G右侧的HMZ必然是root的右子树中的节点,root不在中序遍历的末尾或开始就说明根节点的两颗子树都不为空。
4、观察左子树ADEF,按照前序遍历的顺序来排序为DAFE,因此左子树的根节点为D,并且A是左子树的左子树中的节点,EF是左子树的右子树中的节点。
5、同样的道理,观察右子树节点HMZ,前序为MHZ,因此右子树的根节点为M,左子节点H,右子节点Z。
观察发现,上面的过程是递归的。先找到当前树的根节点,然后划分为左子树,右子树,然后进入左子树重复上面的过程,然后进入右子树重复上面的过程。最后就可以还原一棵树了:
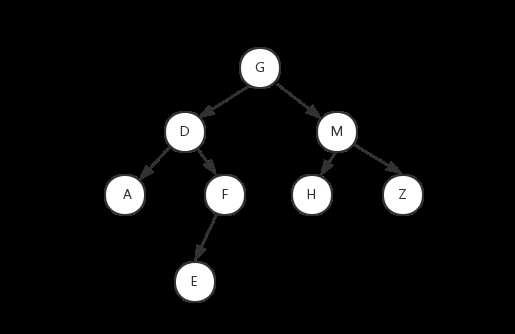
从而得到PostOrder: AEFDHZMG
改进:
更进一步说,其实,如果仅仅要求写后续遍历,甚至不要专门占用空间保存还原后的树。只需要用一个数组保存将要得到的后序,就能实现:
算法2
输入:一个保存后序的数组,前序遍历,中序遍历
1、确定根,放在数组末尾
2、确定左子树的索引范围,放在数组中相同索引的位置。
3、确定右子树索引范围,放在数组中对应索引的位置,刚好能放下。
4、用左子树的前序遍历和中序遍历,把后序遍历保存在对应索引的位置
5、用左子树的前序遍历和中序遍历,把后序遍历保存在对应索引的位置
引申问题
同样我们可以用中序遍历和后序遍历还原这颗树。
然而,如果是前序遍历和后序遍历,就不能够还原这棵树了,因为无法找到中间点,注意下面这两种情况:
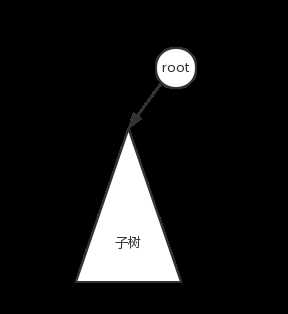
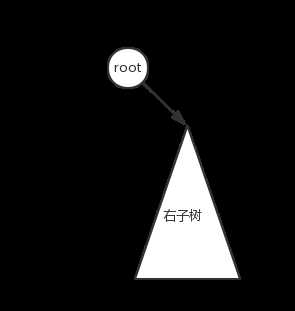
两棵树的前序是相同的,两棵树的后序也是相同的。换句话说,如果有一颗子树,它的根节点的一个子树是空树,那么就无法判定那一个子树是空树。
题干:
输入二叉树的前序遍历和中序遍历的结果,请重建出该二叉树,假设输入的前序遍历和中序的遍历的结果都不包含重复的数字。
