用来求解一般模线性方程,,
X %M1 == A1;
X %M2 == A2;
X %M3 == A3;
。。。。。
当M1, M2, M3,。。。互质时(关于不互质下面会提到),可以利用中国剩余定理求解。。
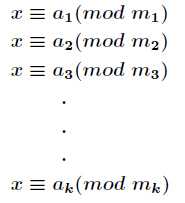
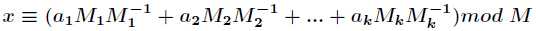
其中



http://acm.hdu.edu.cn/showproblem.php?pid=1370
1 #include <stdio.h> 2 using namespace std; 3 int n, s[4], x, y, d, w, b[] = {23, 28, 33}; 4 void exgcd(int a, int b, int& d, int& x, int& y){ 5 if(!b) d = a, x = 1, y = 0; 6 else exgcd(b, a%b, d, y, x), y -= x*(a/b); 7 } 8 int solve(int *s){ 9 int M = 1, sum = 0, Mi; 10 for(int i = 0; i < 3; i++){ 11 s[i]%=b[i]; 12 M*=b[i]; 13 } 14 for(int i = 0; i < 3; i++){ 15 Mi = M/b[i]; 16 exgcd(Mi, b[i], d, x, y); 17 sum = (sum + Mi*x*s[i]) % M; 18 } 19 sum = (M+sum%M)%M - w; 20 if(sum <= 0) sum += 21252; 21 return sum; 22 } 23 int main(){ 24 scanf("%d", &n); 25 while(n--){ 26 int num = 1; 27 while(scanf("%d %d %d %d", &s[0], &s[1], &s[2], &w)){ 28 if(s[0] == -1 && s[1] == -1 && s[2] == -1) break; 29 printf("Case %d: the next triple peak occurs in %d days.\n", num++, solve(s)); 30 } 31 } 32 return 0; 33 }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
http://acm.fzu.edu.cn/problem.php?pid=1402
裸的剩余定理,,,,神奇的是fzu上面用VC可以过,但是用GNUC++却不可以,。。。。。。XXX
1 #include <iostream> 2 #include <stdio.h> 3 using namespace std; 4 #define ll long long 5 ll a[20], b[20], sum; 6 int t; 7 void ex(ll a, ll b, ll& x, ll& y){ 8 if(!b) x = 1, y = 0; 9 else ex(b, a%b, y, x), y -= x*(a/b); 10 } 11 ll Ch(){ 12 ll xx = 0; 13 for(int i = 0; i < t; ++i){ 14 ll sum2 = sum/a[i], x, y; 15 ex(sum2, a[i], x, y); 16 x = (x%a[i] + a[i])%a[i]; 17 xx = (xx + sum2*x*b[i]%sum)%sum; 18 } 19 return xx; 20 } 21 int main(){ 22 while(~scanf("%d", &t)){ 23 sum = 1; 24 for(int i = 0; i < t; ++i){ 25 scanf("%lld%lld", &a[i], &b[i]); 26 sum *= a[i]; 27 } 28 printf("%lld\n", Ch()); 29 } 30 return 0; 31 }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
http://poj.org/problem?id=1006
裸的剩余定理。。。。
1 #include <iostream> 2 using namespace std; 3 int p, e, i, d, sum = 21252, cnt = 0; 4 int a[3] = {924, 759, 644}; 5 int b[3] = {23, 28, 33}; 6 int c[3]; 7 void xg(int a, int b, int &x, int &y){ 8 if(!b) x = 1, y = 0; 9 else xg(b, a%b, y, x), y -= x*(a/b); 10 } 11 void Ch(){ 12 //cout<<23*28*33<<" "<<23*28<<" "<<23*33<<" "<<28*33<<endl; 13 int num = 0, x, y; 14 for(int i = 0; i < 3; ++i){ 15 xg(a[i], b[i], x, y); 16 x = (x%b[i] + b[i])%b[i]; 17 num = (num + x*a[i]*c[i]%sum)%sum; 18 } 19 int xx = num - d; 20 if(xx <= 0) xx += sum; 21 printf("Case %d: the next triple peak occurs in %d days.\n", ++cnt, xx); 22 //printf("%d\n", xx); 23 } 24 int main(){ 25 while(scanf("%d%d%d%d", &p, &e, &i, &d)){ 26 if(p == -1 && e == -1 && i == -1 && d == -1) break; 27 c[0] = p % 23, c[1] = e % 28, c[2] = i % 33; 28 Ch(); 29 } 30 return 0; 31 }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
http://acm.hdu.edu.cn/showproblem.php?pid=5768
求X, Y之间减去(除pi余ai)后被7整除的数
剩余定理加容斥,。。。。涉及到枚举子集。。。
AC不易啊!!!!!
1 #include <iostream> 2 using namespace std; 3 #define ll long long 4 const int maxn = 20; 5 int n; 6 ll xxx, yyy, a[maxn], p[maxn]; 7 int b[maxn]; 8 void xg(ll a, ll b, ll &x, ll &y){ 9 if(!b) x = 1, y = 0; 10 else xg(b, a%b, y, x), y -= x*(a/b); 11 } 12 ll Ch(int xx){ 13 int w; 14 ll sum = 7LL, x, y, sum2, num = 0; 15 for(int i = 0; i < xx; ++i){ 16 w = b[i]; 17 sum *= p[w]; 18 } 19 for(int i = 0; i < xx; ++i){ 20 w = b[i]; 21 sum2 = sum/p[w]; 22 xg(sum2, p[w], x, y); 23 x = (x%p[w]+p[w])%p[w]; 24 num = (num + x*sum2%sum*a[w]%sum)%sum; 25 } 26 return (yyy-num+sum)/sum - (xxx-num+sum)/sum; 27 } 28 ll solve(){ 29 ll sum = yyy/7 - xxx/7; 30 ll len = 1LL << n; 31 for(int i = 1; i < len; ++i){ 32 int num = 0; 33 for(int j = 0; j < n; ++j){ 34 if(i&(1<<j)) b[num++] = j; 35 } 36 if(num&1) sum -= Ch(num); 37 else sum += Ch(num); 38 } 39 return sum; 40 } 41 int main(){ 42 int t; 43 scanf("%d", &t); 44 for(int j = 1; j <= t; ++j){ 45 scanf("%d%lld%lld", &n, &xxx, &yyy); 46 xxx--; 47 for(int i = 0; i < n; ++i){ 48 scanf("%lld%lld", p+i, a+i); 49 } 50 printf("Case #%d: %lld\n", j, solve()); 51 } 52 return 0; 53 }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
当M1, M2, M3.。。不互质时,该怎么求解呢?
通过合并方程可以求解,,
转载:
/**********************一般模线性方程组***********************/
同样是求这个东西。。
X mod m1=r1
X mod m2=r2
...
...
...
X mod mn=rn
首先,我们看两个式子的情况
X mod m1=r1……………………………………………………………(1)
X mod m2=r2……………………………………………………………(2)
则有
X=m1*k1+r1………………………………………………………………(*)
X=m2*k2+r2
那么 m1*k1+r1=m2*k2+r2
整理,得
m1*k1-m2*k2=r2-r1
令(a,b,x,y,m)=(m1,m2,k1,k2,r2-r1),原式变成
ax+by=m
熟悉吧?
此时,因为GCD(a,b)=1不一定成立,GCD(a,b) | m 也就不一定成立。所以应该先判 若 GCD(a,b) | m 不成立,则!!!方程无解!!!。
否则,继续往下。
解出(x,y),将k1=x反代回(*),得到X。
于是X就是这两个方程的一个特解,通解就是 X‘=X+k*LCM(m1,m2)
这个式子再一变形,得 X‘ mod LCM(m1,m2)=X
这个方程一出来,说明我们实现了(1)(2)两个方程的合并。
令 M=LCM(m1,m2),R=r2-r1
就可将合并后的方程记为 X mod M = R。
然后,扩展到n个方程。
用合并后的方程再来和其他的方程按这样的方式进行合并,最后就能只剩下一个方程 X mod M=R,其中 M=LCM(m1,m2,...,mn)。
那么,X便是原模线性方程组的一个特解,通解为 X‘=X+k*M。
如果,要得到X的最小正整数解,就还是原来那个方法:
X%=M;
if (X<0) X+=M;
例题
http://poj.org/problem?id=2891
1 #include <iostream> 2 using namespace std; 3 #define ll long long 4 const int maxn = 1e5+10; 5 ll p[maxn], a[maxn], t; 6 void ex(ll a, ll b, ll &d, ll &x, ll &y){ 7 if(!b) d = a, x = 1, y = 0; 8 else ex(b, a%b, d, y, x), y -= x*(a/b); 9 } 10 ll solve(){ 11 ll b = p[0], c = a[0], d, x, y, M; 12 for(int i = 1; i < t; ++i){ 13 ll xx = a[i] - c; 14 ex(b, p[i], d, x, y); 15 if(xx % d){ 16 return -1; 17 } 18 //cout<<x<<" "<<y<<"&&&"<<d<<endl; 19 x = (xx/d*x)%(p[i]/d); 20 //cout<<x<<"***"<<endl; 21 c = b*x+c, b = b/d*p[i], c %= b; 22 //cout<<c<<" "<<b<<endl; 23 } 24 return c <= 0 ? c+b : c; 25 } 26 int main(){ 27 while(~scanf("%lld", &t)){ 28 for(int i = 0; i < t; ++i){ 29 scanf("%lld%lld", p+i, a+i); 30 } 31 printf("%lld\n", solve()); 32 } 33 return 0; 34 }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
http://acm.hdu.edu.cn/showproblem.php?pid=1573
中文题
1 #include <iostream> 2 using namespace std; 3 int n, m; 4 int p[11], a[11]; 5 void ex(int a, int b, int &d, int &x, int &y){ 6 if(!b) d = a, x = 1, y = 0; 7 else ex(b, a%b, d, y, x), y -= x*(a/b); 8 } 9 int solve(){ 10 int b = p[0], c = a[0], d, x, y; 11 for(int i = 1; i < m; ++i){ 12 ex(b, p[i], d, x, y); 13 int xx = a[i] - c; 14 //cout<<i<<" "<<a[i]<<" "<<c<<" "<<xx<<" "<<d<<endl; 15 if(xx%d){ 16 return 0; 17 } 18 x = xx/d*x; 19 int w = p[i]/d; 20 x = (x%w+w)%w; 21 c +=x*b, b = b/d*p[i], c %= b; 22 } 23 c = (c > 0 ? c : c+b); 24 if(c > n) return 0; 25 else{ 26 return max((n-c)/b, 0)+1; 27 } 28 } 29 int main(){ 30 int t; 31 scanf("%d", &t); 32 for(int i = 0; i < t; ++i){ 33 scanf("%d%d", &n, &m); 34 for(int j = 0; j < m; ++j){ 35 scanf("%d", p+j); 36 } 37 for(int j = 0; j < m; ++j){ 38 scanf("%d", a+j); 39 } 40 printf("%d\n", solve()); 41 } 42 return 0; 43 }
只有不断学习才能进步!
原文:https://www.cnblogs.com/wenbao/p/5971406.html