博客作业03--栈和队列

1.学习总结(2分)

1.1 写出你认为本周学习中比较重要的知识点关键词，如逻辑结构、栈、队列、存储结构等。

1.栈
（1）栈的定义及操作，包括：建栈，初始化栈，入栈，出栈，判断栈是否为空，取栈顶元素，销毁
（2）顺序储存结构
（3）链式存储结构
（4）栈的应用：表达式求值，求解迷宫问题
2.队列
（1）队列定义：建队列，初始化队列，入队，出队，判断队是否为空，销毁
（2）顺序存储结构，环形队列
（3）链式存储结构
（4）队列的应用：求解报数问题，求解迷宫问题

1.2 使用思维导图将这些关键词组织起来。

2.PTA实验作业（4分）

题目1：jmu-字符串是否对称

设计思路（伪代码或流程图）

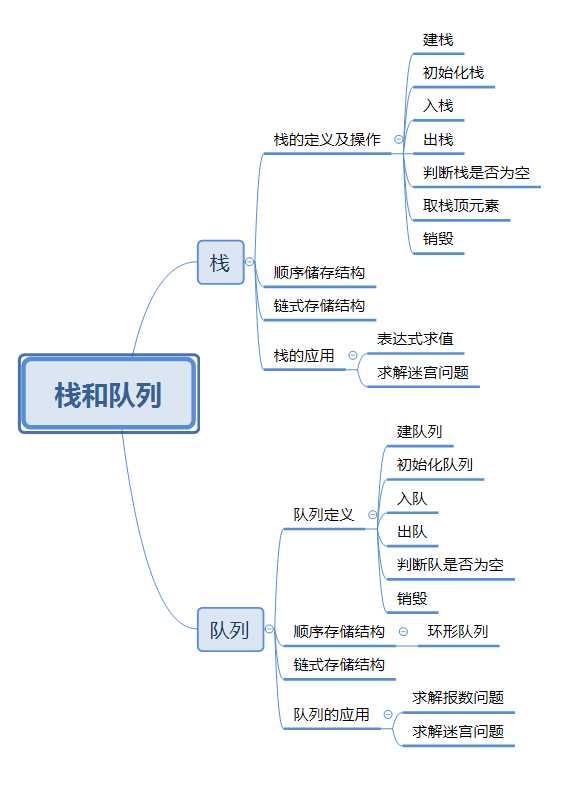
主函数：
定义栈并初始化s
定义字符数组存初始字符串ch
输入初始字符串到数组中
for(i=0;ch[i];i++)
    if(栈为空时)入栈ch[i]
    else if(栈顶元素等于ch[i])出栈
    else 入栈ch[i]
end
if(栈为空)输出yes
else 输出no

代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

PTA提交列表说明。

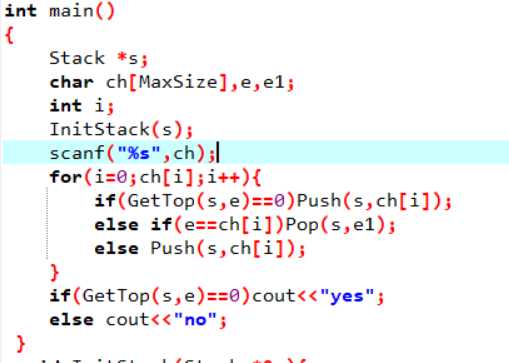
这道题还是挺简单的，刚开始还不太懂栈的应用，所以写的是全部存入栈中再全部拿出，进行比较，虽然也对了，但是明显比现在的方法复杂，于是用现在的方法又写了一遍。

题目2：jmu-报数游戏

设计思路（伪代码或流程图）

主函数：
定义循环变量i，队列总元素n，输出第几个元素m
定义空队列
输入n和m
for(i=0;i<n;i++)
    存入初始队列
if(m大于队列总长）输出错误提示
else 运行函数output，输出报数队列

output函数：
定义计数器cnt，e存队列元素，flag判断是否输出空格
while（队列还不为空）
    cnt++
    if（cnt等于要报数的第m）
        出队列，元素存到e
        输出e，cnt归零
    else
        出队列再进队列
end
        

代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

PTA提交列表说明。

这道题也是比较简单的，一开始做的时候，不知道用队列要怎么做，没有思路想了很久，后来翻了翻课本，知道了，可以将队首元素出列，再入列到队尾，模拟循环的情况，知道了思路一下子就写出来了。

题目3：银行业务队列简单模拟

设计思路（伪代码或流程图）

主函数：
定义两个队列表示A，B
定义数组，并输入原始人群队列
for(i=0;i<n;i++)
    if(数组元素是奇数)进队列B
    else 进队列A
end
while(A和B窗口有一个不为空)
    if(A不为空)
        出队列并输出两个A窗口元素
    if(B不为空)
        出队列并输出一个B窗口元素
end

代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

PTA提交列表说明。

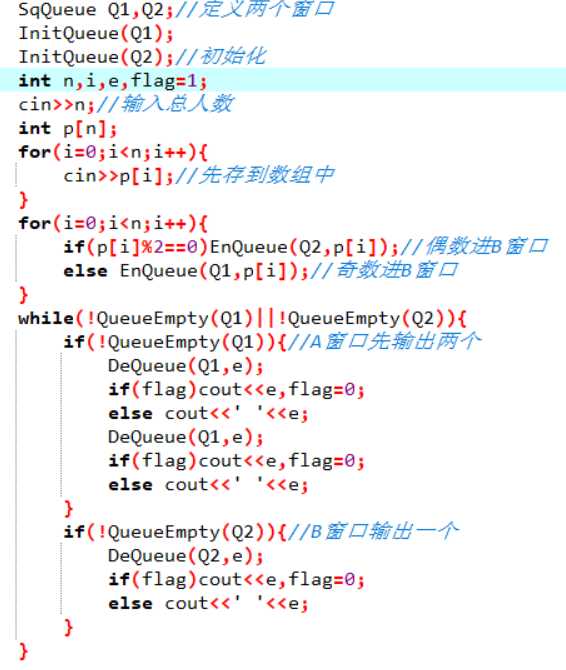
第一个错误是是最大随机N的点错误，后来加大了队列可能达到的最大长度，就对了。

3.截图本周题目集的PTA最后排名（3分）

3.1 栈PTA排名

3.2 队列PTA排名

3.3 我的总分：253

4. 阅读代码（必做，1分）

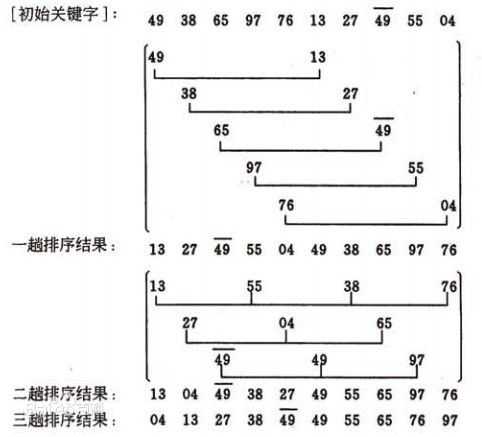
题目描述：希尔排序

#include<stdio.h>
#include<math.h>
 
#define MAXNUM 10
 
void main()
{
    void shellSort(int array[],int n,int t);//t为排序趟数
    int array[MAXNUM],i;
    for(i=0;i<MAXNUM;i++)
        scanf("%d",&array[i]);
    shellSort(array,MAXNUM,(int)(log(MAXNUM+1)/log(2)));//排序趟数应为log2(n+1)的整数部分
    for(i=0;i<MAXNUM;i++)
        printf("%d ",array[i]);
    printf("\n");
}
 
//根据当前增量进行插入排序
void shellInsert(int array[],int n,int dk)
{
    int i,j,temp;
    for(i=dk;i<n;i++)//分别向每组的有序区域插入
    {
        temp=array[i];
        for(j=i-dk;(j>=i%dk)&&array[j]>temp;j-=dk)//比较与记录后移同时进行
            array[j+dk]=array[j];
        if(j!=i-dk)
            array[j+dk]=temp;//插入
    }
}
 
//计算Hibbard增量
int dkHibbard(int t,int k)
{
    return (int)(pow(2,t-k+1)-1);
}
 
//希尔排序
void shellSort(int array[],int n,int t)
{
    void shellInsert(int array[],int n,int dk);
    int i;
    for(i=1;i<=t;i++)
        shellInsert(array,n,dkHibbard(t,i));
}

分析：
希尔排序(Shell‘s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
算法过程：
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量 =1( < …<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

该算法若数据基本有序且记录较少时，当文件初态基本有序时直接插入排序所需的比较和移动次数均较少，效率是非常好的，但是数据一多就有不可靠性，由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

5. 代码Git提交记录截图

博客作业03--栈和队列

原文：https://www.cnblogs.com/doimpossible/p/8735567.html