带权路劲长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值Wk,从根结点到每个叶子结点的长度为Ik,则每个叶子结点的带权路径长度之和就是: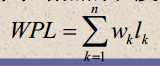
最优二叉树或哈夫曼树:WPL最小的二叉树
哈夫曼树的特点:
没有度为1的结点;
n个叶子结点的哈夫曼树共有2n-1个结点;
哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树;
对同一组权值{W1,W2,......,Wn},是否存在不同构的两颗哈夫曼树呢?
算法:
1 typedef struct TreeNode *HuffmanTree; 2 struct TreeNode { 3 int Weight; 4 HuffmanTree Left, Right; 5 }; 6 7 HuffmanTree Huffman(MinHeap H) 8 { 9 /* 假设H->Size个权值已经存在H->Elements[]->Weight里 */ 10 int i, HuffmanTree T; 11 BuildMinHeap(H); /* 将H->Elements[]按权值调整为最小堆 */ 12 for(i=1;i<H->Size;i++) { /* 做H->Size-1次合并 */ 13 T = malloc(sizeof(struct TreeNode)); /* 建立新结点 */ 14 T->Left = DeleteMin(H); /* 从最小堆中删除一个结点,作为新T的左子结点 */ 15 T->Right = DeleteMin(H); /* 从最小堆中删除一个结点,作为新T的右子结点 */ 16 T->Weight = T->Left->Weight+T->Right->Weight; /* 计算新权值 */ 17 Insert(H, T); /* 将新T插入最小堆 */ 18 } 19 T = DeleteMin(H); 20 return T; 21 }
原文:https://www.cnblogs.com/ch122633/p/8847217.html