[CEOI2008]order
题目描述:
有N个任务,M种机器,每种机器你可以租或者买过来.
每个工作包括若干道工序,每道工序需要某种机器来完成,你可以通过购买或租用机器来完成。
现在给出这些参数,求最大利润
输入格式:
第一行给出 N, M (1 <= N <= 1200, 1 <= M <= 1200) 下面将有N个任务的数据。
每组数据第一行给出完成这个任务能赚到的钱([1,5000])及有多少道工序
接下来若干行每行两个数,分别描述完成工序所需要的机器编号及租用它的费用([1,20000])
最后M行,每行给出购买机器的费用([1,20000])
输出格式:
最大利润
题解?
也许吧,学习大佬的风格,采用简短的话语来描述。
也算是一种记录吧.
本题,额,比较简单的最小割。
把图抽象出来:
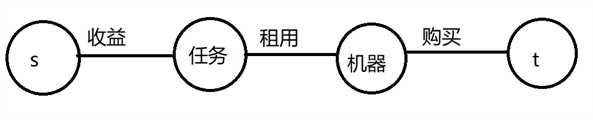
分析割(最小割):
对于每一个任务,割掉s与它的连边意味着无需后面的额外花费
对于每一个机器,如果购买了,那么租用的边不可能被割掉(最小)
对于每一个机器,如果未购买,可以选择对于每个选择的任务单独租用
也就是说,图可以保证让花费最小
那么总收益 - 最小花费 = 最大收益
注意常数因子,朴素Dinic可能无法通过
代码如下:
#include <cstdio>
#define sid 200050
#define ssd 3000500
#define ri register int
using namespace std;
inline int read() {
int p = 0, w = 1;
char c = getchar();
while(c > ‘9‘ || c < ‘0‘) {
if(c == ‘-‘) w = -1;
c = getchar();
}
while(c >= ‘0‘ && c <= ‘9‘) {
p = p * 10 + c - ‘0‘;
c = getchar();
}
return p * w;
}
inline int min(int a, int b) {
return (a < b) ? a : b;
}
int n, m, s, t, cnt = 1;
int lev[sid], cap[sid], cur[sid], q[sid];
int nxt[ssd], res[ssd], node[ssd], mark[sid];
inline void Unicom(int u, int v, int w) {
nxt[++ cnt] = cap[u]; cap[u] = cnt;
node[cnt] = v; res[cnt] = w;
nxt[++ cnt] = cap[v]; cap[v] = cnt;
node[cnt] = u; res[cnt] = 0;
}
inline void Bfs() {
++ mark[1];
for(ri i = 1; i <= t; i ++) cur[i] = cap[i];
int fr = 1, to = 2;
q[fr] = t; lev[t] = 1;
while(fr <= to) {
int e = q[fr ++];
for(ri i = cap[e]; i; i = nxt[i]) {
int d = node[i];
if(lev[d] || !res[i ^ 1]) continue;
lev[d] = lev[e] + 1; ++ mark[lev[d]];
q[++ to] = d;
}
}
}
inline int Dfs(int e, int ff) {
int tmp, tt = 0;
if(e == t) return ff;
for(int &i = cur[e]; i; i = nxt[i]) {
int d = node[i];
if(lev[e] != lev[d] + 1) continue;
tmp = Dfs(d, min(ff, res[i]));
tt += tmp; ff -= tmp;
res[i] -= tmp; res[i ^ 1] += tmp;
if(!ff) return tt;
}
if(!(-- mark[lev[e]])) lev[s] = t + 1;
++ mark[++ lev[e]]; cur[e] = cap[e];
return tt;
}
inline int ISAP() {
Bfs();
int ans = Dfs(s, 1e9);
while(lev[s] <= t) ans += Dfs(s, 1e9);
return ans;
}
int main() {
n = read(); m = read();
int sum = 0;
s = n + m + 1; t = s + 1;
for(ri i = 1; i <= n; i ++) {
int pw = read(), pn = read();
sum += pw; Unicom(s, i, pw);
for(ri j = 1; j <= pn; j ++) {
int u = read(), w = read();
Unicom(i, u + n, w);
}
}
for(ri i = 1; i <= m; i ++) Unicom(n + i, t, read());
printf("%d\n", sum - ISAP());
return 0;
}
原文:https://www.cnblogs.com/reverymoon/p/8858066.html