变量说明:
设 为一组随机变量,这些随机变量构成随机向量
为一组随机变量,这些随机变量构成随机向量



 (1)
(1)
当中

单随机变量间的协方差:
随机变量
 (2)
(2)
依据已知的样本值能够得到协方差的预计值例如以下:
 (3)
(3)
能够进一步地简化为:
 (4)
(4)

 (5)
(5)
当中
假设全部样本的均值为一个零向量,则式(5)能够表达成:
 (6)
(6)
补充说明:
1、协方差矩阵中的每个元素是表示的随机向量X的不同分量之间的协方差,而不是不相同本之间的协方差,如元素Cij就是反映的随机变量Xi, Xj的协方差。
2、协
方差是反映的变量之间的二阶统计特性,假设随机向量的不同分量之间的相关性非常小,则所得的协方差矩阵差点儿是一个对角矩阵。对于一些特殊的应用场合,为了使
随机向量的长度较小,能够採用主成分分析的方法,使变换之后的变量的协方差矩阵全然是一个对角矩阵,之后就能够舍弃一些能量较小的分量了(对角线上的元素
反映的是方差,也就是交流能量)。特别是在模式识别领域,当模式向量的维数过高时会影响识别系统的泛化性能,常常须要做这种处理。
3、必须注意的是,这里所得到的式(5)和式(6)给出的仅仅是随机向量协方差矩阵真实值的一个预计(即由所測的样本的值来表示的,随着样本取值的不同会发生变化),故而所得的协方差矩阵是依赖于採样样本的,而且样本的数目越多,样本在整体中的覆盖面越广,则所得的协方差矩阵越可靠。
在概率论和统计学中,相关或称相关系数或关联系数,显示两个随机变量之间线性关系的强度和方向。在统计学中,相关的意义是用来衡量两个变量相对于其相互独立的距离。在这个广义的定义下,有很多依据数据特点而定义的用来衡量数据相关的系数。
对于不同数据特点,能够使用不同的系数。最经常使用的是皮尔逊积差相关系数。其定义是两个变量协方差除以两个变量的标准差(方差)。
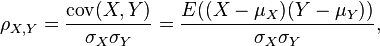
由于μX = E(X),σX2 = E(X2) ? E2(X),相同地,对于Y,能够写成

当两个变量的标准差都 不为零,相关系数才有定义。从柯西—施瓦茨不等式可知,相关系数不超过1. 当两个变量的线性关系增强时,相关系数趋于1或-1。当一个变量添加而还有一变量也添加时,相关系数大于0。当一个变量的添加而还有一变量降低时,相关系数小 于0。当两个变量独立时,相关系数为0.但反之并不成立。 这是由于相关系数只反映了两个变量之间是否线性相关。比方说,X是区间[-1,1]上的一个均匀分布的随机变量。Y = X2. 那么Y是全然由X确定。因此Y 和X是不独立的。可是相关系数为0。或者说他们是不相关的。当Y 和X服从联合正态分布时,其相互独立和不相关是等价的。
当一个或两个变量带有測量误差时,他们的相关性就受到削弱,这时,“反衰减”性(disattenuation)是一个更准确的系数。
原文:http://www.cnblogs.com/mfrbuaa/p/3844817.html