圆桌骑士。有的骑士之间是相互憎恨的,不能连坐,需要安排奇数个骑士围着桌子坐着,大于3个,求哪些骑士不可能安排到座位。
根据给定的关系,如果两个骑士之间没有憎恨关系,那么连边。最终就是求有多少个点无法位于奇圈之内。
首先求所有联通分量,对于每个连通分量二分图染色,看看是否存在一个奇圈,如果有一个,那么这个联通分量里面的所有点都可以在至少一个奇圈之内。(详细的见白书)
下面重点说说如何找联通分量的。
方法是用一个栈来维护下面走过的边,如果当前点是割点,那么把在这个点后面加入的边全部退出来,把这些点拿出来,就构成了一个独立的联通分量。
这个维护是很有意思的,因为是递归操作,有点难以理解。
结合下面的图来说:
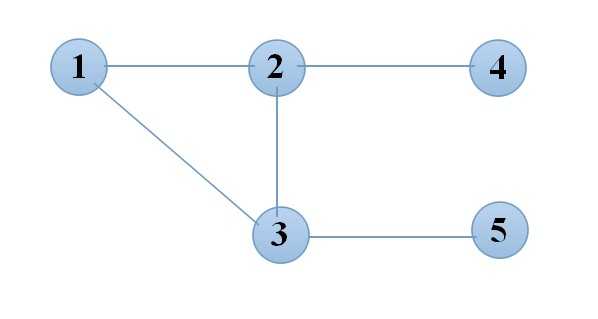
这也就是题目的样例,如图,假设我们现在走1->2->4,现在2是关键点,于是就把2->4这条边出来,(2,4)两个点构成一个分量。
同理的有3,5。
但是问题也许会是,我一开是走的是1->2->3->5,那么会不会导致(2,3,5)构成一个分量,不会的!因为在你处理完3后,3->5这条边就已经被拿出来了,最终也只有(1,2,3)。这个递归和栈的混合运用是有一点难以理解,好好想想就清楚了。
还有一个问题,2-4并不能看成是一个双联通分量,但是在这个题目里面不会对答案产生影响,因为2个点也无法构成奇圈(3个点呢?嘿嘿不会有3个点的情况)。想想就知道了,加油!
召唤代码君:
#include <iostream> #include <cstdio> #include <cstring> #include <vector> #define maxn 2000100 using namespace std; vector<int> bcc[maxn]; int next[maxn],first[1010],to[maxn],edge; int low[1010],d[1010],belong[1010],color[1010]; int a[1010][1010]; int n,m,T=0,bccnum,ans,u,v,dfs_clock; int U[maxn],V[maxn],top; bool can[1010]; void _init() { T++,ans=dfs_clock=bccnum=top=0,edge=-1; for (int i=1; i<=n; i++) low[i]=d[i]=belong[i]=first[i]=-1,can[i]=false; } void addedge(int uu,int vv) { edge++; to[edge]=vv,next[edge]=first[uu],first[uu]=edge; edge++; to[edge]=uu,next[edge]=first[vv],first[vv]=edge; } bool find(int cur,int tag) { for (int i=first[cur]; i!=-1; i=next[i]) { if (belong[to[i]]!=tag) continue; if (color[to[i]]==color[cur]) return true; if (color[to[i]]!=-1) continue; color[to[i]]=1-color[cur]; if (find(to[i],tag)) return true; } return false; } void dfs(int cur,int fa) { low[cur]=d[cur]=++dfs_clock; for (int i=first[cur]; i!=-1; i=next[i]) { if ((i^1)==fa) continue; if (d[to[i]]==-1) { U[++top]=cur,V[top]=to[i]; dfs(to[i],i); low[cur]=min(low[cur],low[to[i]]); if (low[to[i]]>=d[cur]) { bcc[++bccnum].clear(); for (;;top--) { if (belong[U[top]]!=bccnum) belong[U[top]]=bccnum,bcc[bccnum].push_back(U[top]); if (belong[V[top]]!=bccnum) belong[V[top]]=bccnum,bcc[bccnum].push_back(V[top]); if (U[top]==cur && V[top]==to[i]) { top--; break; } } for (unsigned j=0; j<bcc[bccnum].size(); j++) color[bcc[bccnum][j]]=-1; color[bcc[bccnum][0]]=1; if (find(bcc[bccnum][0],bccnum)) for (unsigned j=0; j<bcc[bccnum].size(); j++) can[bcc[bccnum][j]]=true; } } else low[cur]=min(low[cur],low[to[i]]); } } int main() { while (scanf("%d%d",&n,&m) && (n|m)) { _init(); while (m--) { scanf("%d%d",&u,&v); a[u][v]=a[v][u]=T; } for (int i=1; i<=n; i++) for (int j=i+1; j<=n; j++) if (a[i][j]!=T) addedge(i,j); for (int i=1; i<=n; i++) if (d[i]==-1) dfs(i,-1); for (int i=1; i<=n; i++) if (!can[i]) ans++; printf("%d\n",ans); } return 0; }
UVAlive3523_Knights of the Round Table,布布扣,bubuko.com
UVAlive3523_Knights of the Round Table
原文:http://www.cnblogs.com/Canon-CSU/p/3847707.html