1 判断一个数是否为素数
对于判断一个数m是否为素数,最朴素的方式是按照素数的定义,试除以从2开始到m-1的整数,倘若无一例外地不能整除,则该数必为素数。
1 #include<iostream> 2 using namespace std; 3 int main() 4 { 5 cout << "Please input a number:\n"; 6 int m; 7 cin >> m; 8 for (int i = 2; i < m;++i)//i从2到m-1 9 if (m%i == 0) 10 { 11 cout << m << " is not a prime.\n"; 12 return 1; 13 } 14 cout << m << " is a prime.\n"; 15 cin.get(); 16 return 0; 17 18 }
下面来深究一下:
在数学上,假定某个整数m不是素数,则一定可以表示成两个因子的积:
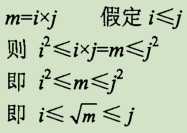
所以必定有一个因子不大于m的平方根(即这里所说的 i)。故判断m是否为素数,只要试除到m的平方根就可以了,不必一直到m-1(这段话请务必理解)。因此,上面的程序可以修改为:
1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 int main() 5 { 6 cout << "Please input a number:\n"; 7 int m; 8 cin >> m; 9 double sqrtm = sqrt(m*1.0); 10 for (int i = 2; i < sqrtm; ++i) 11 if (m%i == 0) 12 { 13 cout << m << " is not a prime.\n"; 14 return 1; 15 } 16 cout << m << " is a prime.\n"; 17 cin.get(); 18 return 0; 19 }
这里取了一个浮点型(double)变量sqrtm,其值为m的平方根,该值是调用了一个C++的库函数sqrt而得,它在cmath中说明。由于i是整数,所以不等式i<=sqrtm中,i只能取小于或等于sqrtm的最大整数。
修改后的程序,效率提高了一些。例如判断101是否为素数,本来要从2试除到100,现在只要从2试除到10就行了。
原文:https://www.cnblogs.com/ariel-dreamland/p/8976187.html