反卷积是指,通过测量输出和已知输入重构未知输入的过程。在神经网络中,反卷积过程并不具备学习的能力,仅仅是用于可视化一个已经训练好的卷积神经网络,没有学习训练的过程。反卷积有着许多特别的应用,一般可以用于信道均衡、图像恢复、语音识别、地震学、无损探伤等未知输入估计和过程辨识方面的问题。
在神经网络的研究中,反卷积更多的是充当可视化的作用,对于一个复杂的深度卷积网络,通过每层若干个卷积核的变换,我们无法知道每个卷积核关注的是什么,变换后的特征是什么样子。通过反卷积的还原,可以对这些问题有个清晰的可视化,以各层得到的特征图作为输入,进行反卷积得到反卷积结果,以验证显示各层提取到的特征图。
反卷积可以理解为卷积操作的逆操作,这里千万不要当成反卷积操作可以复原卷积操作的输入值,反卷积并没有那个功能,它仅仅是将卷积变换过程中的步骤反向变换一次而已,通过将卷积核转置,与卷积后的结果再做一遍卷积,所以它还有一个名字叫做转置卷积。
举个例子:假如你想要查看Alexnet 的conv5提取到了什么东西,我们就用conv5的特征图后面接一个反卷积网络,然后通过:反池化、反激活、反卷积,这样的一个过程,把本来一张13*13大小的特征图(conv5大小为13*13),放大回去,最后得到一张与原始输入图片一样大小的图片(227*227)。
虽然它不能还原出原来卷积的样子,但是在作用上有类似的效果,你可以将带有小部分缺失的信息最大化的恢复,也可以用来恢复被卷积生成后的原始输入。
反卷积的具体操作比较复杂,这里不介绍如何具体实现反卷积,在tensorflow中反卷积的是通过函数tf.nn.conv2d_transpose()来实现的:
def conv2d_transpose(value, filter, output_shape, strides, padding="SAME", data_format="NHWC", name=None):
具体参数说明如下:
返回反卷积后的形状,按照output_shape指定的形状。
查看该函数的实现代码,我们可以看到反卷积的操作其实是使用了gen_nn_ops.conv2d_backprop_input()函数来实现的,相当于在TensorFlow中利用了卷积操作在反向传播的处理函数中做反卷积操作,即卷积操作的反向传播就是反卷积操作。
我们通过对模拟数据进行卷积核反卷积的操作,来比较卷积与反卷积中padding在SAME和VALID下的变化。先定义一个[1,4,4,1]的矩阵,矩阵里的元素值都为1,与滤波器大小为2x2,步长为2x2,分别使用padding为SAME和VALID两种情况生成卷积数据,然后将结果再进行反卷积运算,打印输出的结果
‘‘‘ 一 反卷积实例 ‘‘‘ import tensorflow as tf import numpy as np #模拟数据 img = tf.Variable(tf.constant(1.0,shape=[1,4,4,1])) kernel =tf.Variable(tf.constant([1.0,0,-1,-2],shape=[2,2,1,1])) #分别进行VALID和SAME操作 conv = tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding=‘VALID‘) cons = tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding=‘SAME‘) #VALID填充计算方式 (n - f + 1)/s向上取整 print(conv.shape) #SAME填充计算方式 n/s向上取整 print(cons.shape) #在进行反卷积操作 contv = tf.nn.conv2d_transpose(conv,kernel,[1,4,4,1],strides=[1,2,2,1],padding=‘VALID‘) conts = tf.nn.conv2d_transpose(cons,kernel,[1,4,4,1],strides=[1,2,2,1],padding=‘SAME‘) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) print(‘kernel:\n‘,sess.run(kernel)) print(‘conv:\n‘,sess.run(conv)) print(‘cons:\n‘,sess.run(cons)) print(‘contv:\n‘,sess.run(contv)) print(‘conts:\n‘,sess.run(conts))
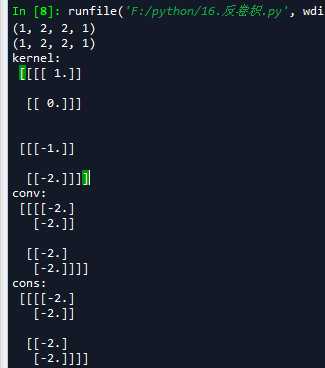
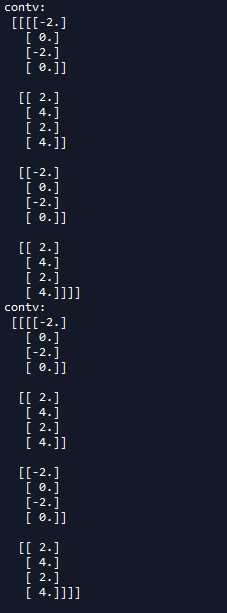
我们可以把padding为VALID方式时的卷积核反卷积操作绘制出来,如下图:
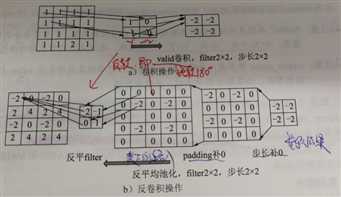
反池化属于池化的逆操作,是无法通过池化的结果还原出全部的原始数据,因此池化的过程只保留主要信息,舍去部分信息。如果想从池化后的这些主要信息恢复出全部信息,由于存在着信息缺失,这时只能通过补位来实现最大程度的信息完整。
池化层常用的有最大池化和平均池化,其反池化也需要与其对应。
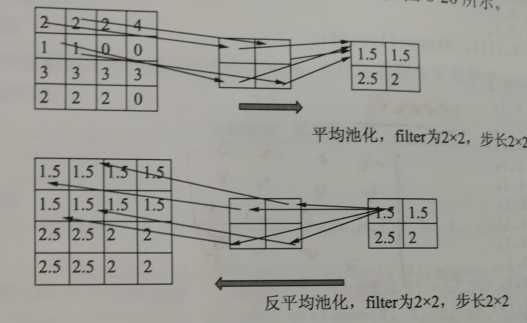
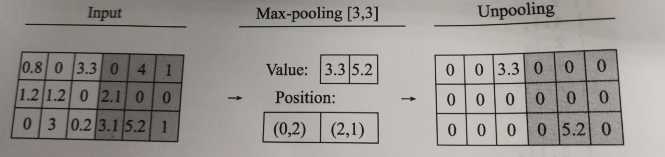
TensorFlow中目前还没有反池化操作的函数。对于最大池化层,也不支持输出最大激活值得位置,但是同样有个池化的反向传播函数tf.nn.max_pool_with_argmax()。该函数可以找出位置,需要开发者利用这个函数做一些改动,自己封装一个最大池化操作,然后再根据mask写出反池化函数。
‘‘‘ 二 反池化操作 ‘‘‘ def max_pool_with_argmax(net,stride): ‘‘‘ 重定义一个最大池化函数,返回最大池化结果以及每个最大值的位置(是个索引,形状和池化结果一致) args: net:输入数据 形状为[batch,in_height,in_width,in_channels] stride:步长,是一个int32类型,注意在最大池化操作中我们设置窗口大小和步长大小是一样的 ‘‘‘ #使用mask保存每个最大值的位置 这个函数只支持GPU操作 _, mask = tf.nn.max_pool_with_argmax( net,ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1],padding=‘SAME‘) #将反向传播的mask梯度计算停止 mask = tf.stop_gradient(mask) #计算最大池化操作 net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1],strides=[1, stride, stride, 1], padding=‘SAME‘) #将池化结果和mask返回 return net,mask def un_max_pool(net,mask,stride): ‘‘‘ 定义一个反最大池化的函数,找到mask最大的索引,将max的值填到指定位置 args: net:最大池化后的输出,形状为[batch, height, width, in_channels] mask:位置索引组数组,形状和net一样 stride:步长,是一个int32类型,这里就是max_pool_with_argmax传入的stride参数 ‘‘‘ ksize = [1, stride, stride, 1] input_shape = net.get_shape().as_list() # calculation new shape output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3]) # calculation indices for batch, height, width and feature maps one_like_mask = tf.ones_like(mask) batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1]) b = one_like_mask * batch_range y = mask // (output_shape[2] * output_shape[3]) x = mask % (output_shape[2] * output_shape[3]) // output_shape[3] feature_range = tf.range(output_shape[3], dtype=tf.int64) f = one_like_mask * feature_range # transpose indices & reshape update values to one dimension updates_size = tf.size(net) indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size])) values = tf.reshape(net, [updates_size]) ret = tf.scatter_nd(indices, values, output_shape) return ret #定义一个形状为4x4x2的张量 img = tf.constant([ [[0.0,4.0],[0.0,4.0],[0.0,4.0],[0.0,4.0]], [[1.0,5.0],[1.0,5.0],[1.0,5.0],[1.0,5.0]], [[2.0,6.0],[2.0,6.0],[2.0,6.0],[2.0,6.0]], [[3.0,7.0],[3.0,7.0],[3.0,7.0],[3.0,7.0]], ]) img = tf.reshape(img,[1,4,4,2]) #最大池化操作 pooling1 = tf.nn.max_pool(img,ksize=[1,2,2,1],strides=[1,2,2,1],padding=‘SAME‘) #带有最大值位置的最大池化操作 pooling2,mask = max_pool_with_argmax(img,2) #反最大池化 img2 = un_max_pool(pooling2,mask,2) with tf.Session() as sess: print(‘image:‘) image = sess.run(img) print(image) #默认的最大池化输出 result = sess.run(pooling1) print(‘max_pool:\n‘,result) #带有最大值位置的最大池化输出 result,mask2 = sess.run([pooling2,mask]) print(‘max_pool_with_argmax:\n‘,result,mask2) #反最大池化输出 result = sess.run(img2) print(‘un_max_pool‘,result)
这里我们自己定义了两个函数,一个是带有最大值位置的最大池化函数,一个反最大池化函数,程序运行后,我们应该可以看到自己定义的最大池化与原来的版本输出是一样的,由于tf.nn.max_pool_with_argmax()函数只支持GPU操作,不能在CPU机器上运行,所以我没法运行这段程序。mask的值是将整个数组flat后的索引,并保持与池化结果一致的shape。
在反向传播的过程中,神经网络需要对每个代价函数对应的学习参数求偏导,计算出的这个值叫做梯度,用来乘以学习率然后更新学习参数使用的。它是通过tf.gradients()函数来实现的,这个函数的第一个参数为需要求导的公式,第二个参数为指定公式中的哪个变量来求偏导。如果对一个不存在的变量求偏导,会返回None。
‘‘‘ 三 偏导计算 ‘‘‘ w1 = tf.Variable([[1,2]]) #1x2 w2 = tf.Variable([[3,4]]) #1x2 y = tf.matmul(w1,[[9],[10]]) #2x1 #求w1的梯度 grads = tf.gradients(y,w1) #1x2 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) gradval = sess.run(grads) print(gradval)
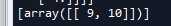
可以看到我们计算得到的结果为[[9,10]],形状为1x2,即[[9],[10]]的转置。至于为什么是其转置,你需要了解一下矩阵如何求偏导的知识。
import numpy as np x = np.array([[9,10]]) print(x.shape) x = np.array([[9],[10]]) print(x.shape)

tf.gradients()函数还可以同时对多个子式求关于多个变量的偏导:
tf.reset_default_graph() w1 = tf.get_variable(‘w1‘,shape=[2]) w2 = tf.get_variable(‘w2‘,shape=[2]) w3 = tf.get_variable(‘w3‘,shape=[2]) w4 = tf.get_variable(‘w4‘,shape=[2]) y1 = w1 + w2 + w3 y2 = w3 + w4 gradients = tf.gradients([y1,y2],[w1,w2,w3,w4],grad_ys=[tf.convert_to_tensor([1.,2.]),tf.convert_to_tensor([3.,4.])]) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) gradval = sess.run(gradients) print(gradval)
上面的程序有两个op,4个参数,演示了使用tf.gradients()函数同时为两个式子4个参数求梯度。

这里使用了tf.gradients()函数的第三个参数,即给定公式结果的值,来求参数梯度,这里相当于y1为[1.,2.],y2为[3.,4.]。对于y1来讲,求关于w1的梯度时,会认为w2和w3为常数,所以w2,w3的导数为0,即w1的梯度就为[1.,2.]。同理可以得出w2,w3均为[1.,2.],接着求y2的梯度,得到w3和w4均为[3.,4.]。然后将两个式子中的w3结果加起来,所以w3就为[4.,6.]。(这一块我也没有懂,一脸懵逼)
对于反向传播过程中某种情况需要停止梯度的运算时,在TensorFlow中提供了一个tf.stop_gradient()函数,被它定义过得节点将没有梯度运算的功能。
‘‘‘ 四 梯度停止 ‘‘‘ w1 = tf.Variable(2.0) w2 = tf.Variable(2.0) a = tf.multiply(w1, 3.0) #停止a节点梯度运算的功能 a_stoped = tf.stop_gradient(a) b = tf.multiply(a_stoped, w2) gradients = tf.gradients(b, xs=[w1, w2]) print(gradients)

可见,一个节点被 stop之后,这个节点上的梯度,就无法再向前BP了。由于w1变量的梯度只能来自a节点,由于停止了1节点梯度运算的功能,所以,计算梯度返回的是None。
a = tf.Variable(1.0) b = tf.Variable(1.0) c = tf.add(a, b) #停止c节点梯度运算的功能 c_stoped = tf.stop_gradient(c) d = tf.add(a, b) e = tf.add(c_stoped, d) gradients = tf.gradients(e, xs=[a, b]) with tf.Session() as sess: tf.global_variables_initializer().run() print(sess.run(gradients))
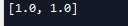
虽然 c节点被stop了,但是a,b还有从d传回的梯度,所以还是可以输出梯度值的。
参考文章:用反卷积(Deconvnet)可视化理解卷积神经网络
tensorflow学习笔记(三十):tf.gradients 与 tf.stop_gradient() 与 高阶导数
第十四节,TensorFlow中的反卷积,反池化操作以及gradients的使用
原文:https://www.cnblogs.com/zyly/p/8991412.html